목차
그래프의 정점을 어떻게 벡터로 표현할까?
정점 표현 학습
정점 표현 학습이란
- 그래프의 정점들을 벡터의 형태로 표현하는 것
- 정점 표현 학습 = 정점 임베딩 (Node Embedding)
- 정점 임베딩은 벡터 형태의 표현 그 자체를 의미
- 정점이 표현되는 벡터 공간을 임베딩 공간이라 부름
- 각 정점 u 에 대한 임베딩, 즉 벡터 표현 $z_u$ 가 정점 임베딩의 출력
왜 정점 임베딩을 사용할까
- 벡터 형태의 데이터를 여러 툴에 사용할 수 있기 때문
- 더이상 그래프 형태로 처리하지 않고 벡터로 처리함으로써 다양한 툴 사용 가능해짐
- 툴 : 분류기 (로지스틱 회귀분석) , 군집 분석 알고리즘, 정점 분류 등
정점 표현 학습의 목표
- 어떤 기준으로 정점을 벡터로 변환할까?
- 그래프에서의 정점간 유사도를 임베딩 공간에서도 보존!
- 임베딩 공간에서의 유사도는 내적을 사용
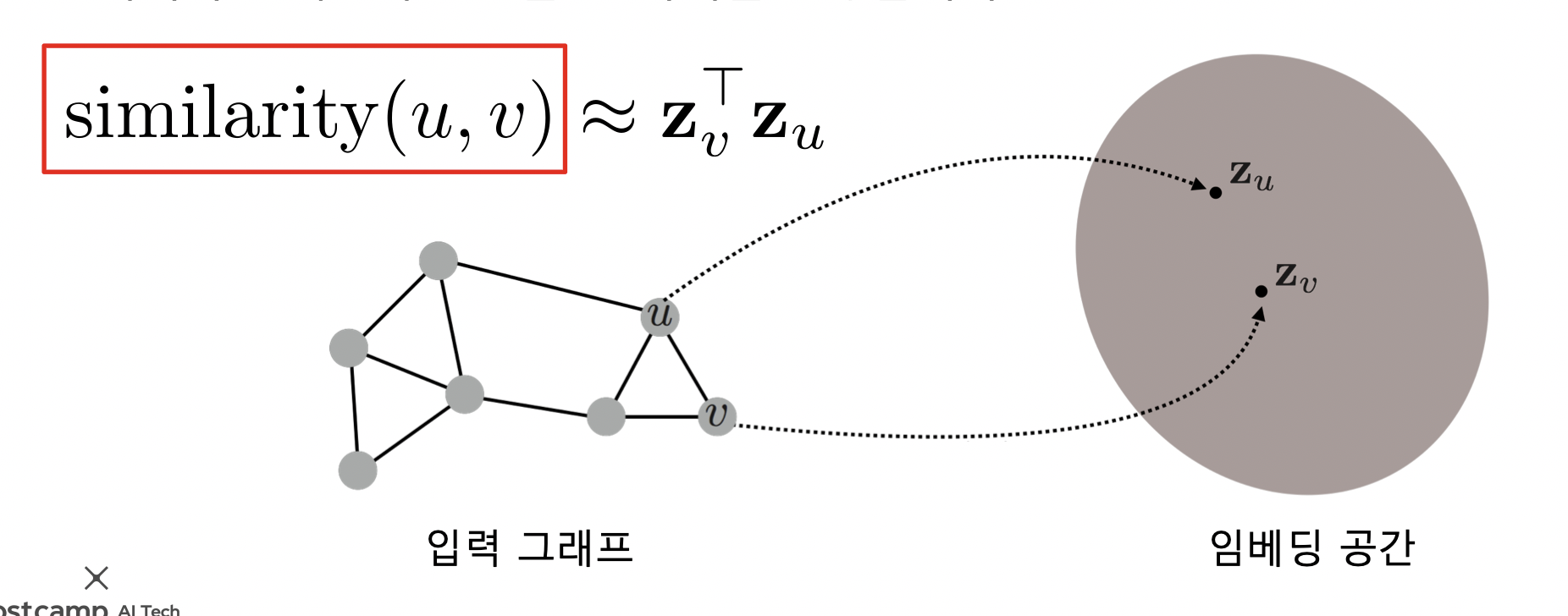
- 내적은 두 벡터가 클 수록, 같은 방향일수록 커짐
- 그래프의 두 정점 간 유사도는 여러가지 방법이 있음
- 인접성 기반 접근법
- 거리/경로/중첩 기반 접근법
- 임의보행 기반 접근법
- 정리
- 그래프에서 정점 유사도를 정의
- 정의한 유사도를 보존하도록 정점 임베딩 학습
인접성 기반 접근법
인접성 기반 접근법이란
- 그래프의 두 정점 간 유사도를 인접행렬로 나타냄
- 인접성 (Adjacency) 기반 접근법에서는 두 정점이 인접할 때 유사하다고 간주
- 두 정점 u 와 v 가 인접하다는 뜻은 둘을 직접 연결하는 간선 (u, v) 가 있음
- 인접행렬로 간선이 있으면 1, 없으면 0 으로 표현
- 인접성 기반 접근법의 손실함수가 최소화되는 정점 임베딩을 찾는 것이 목표
- 최소화 기법으로 SGD 등 사용
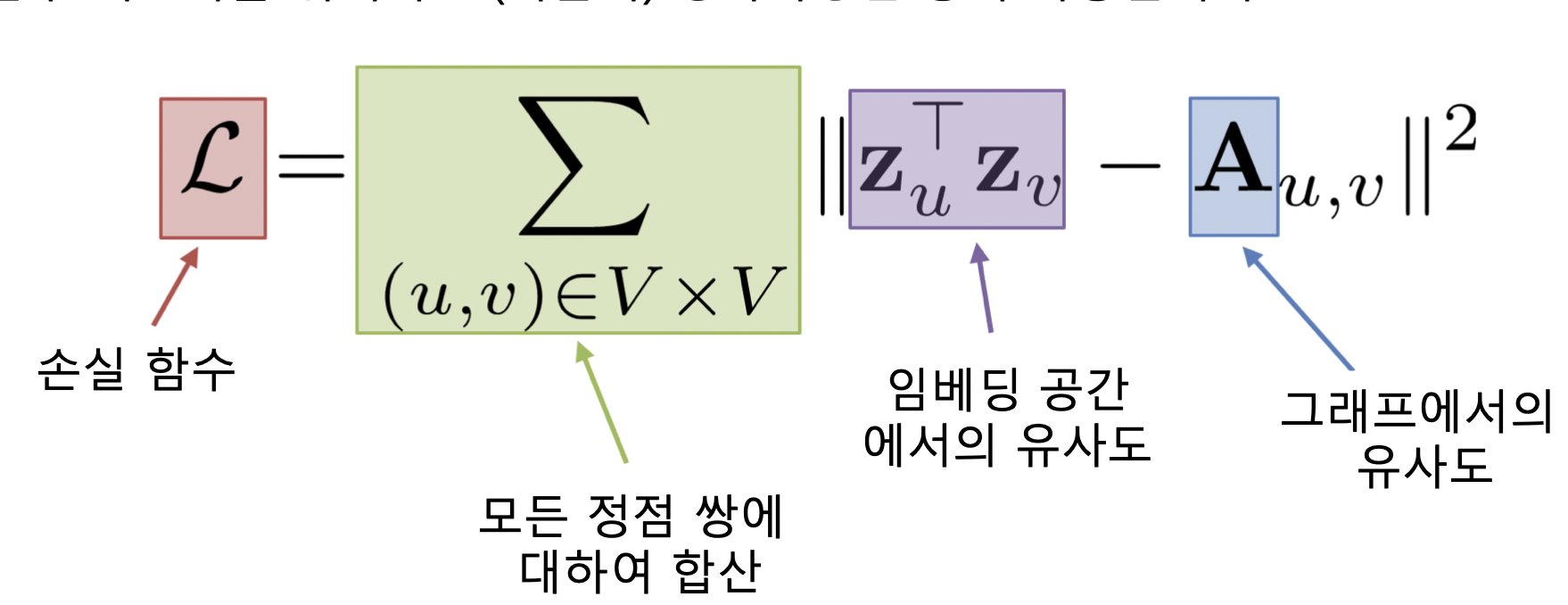
-
한계점
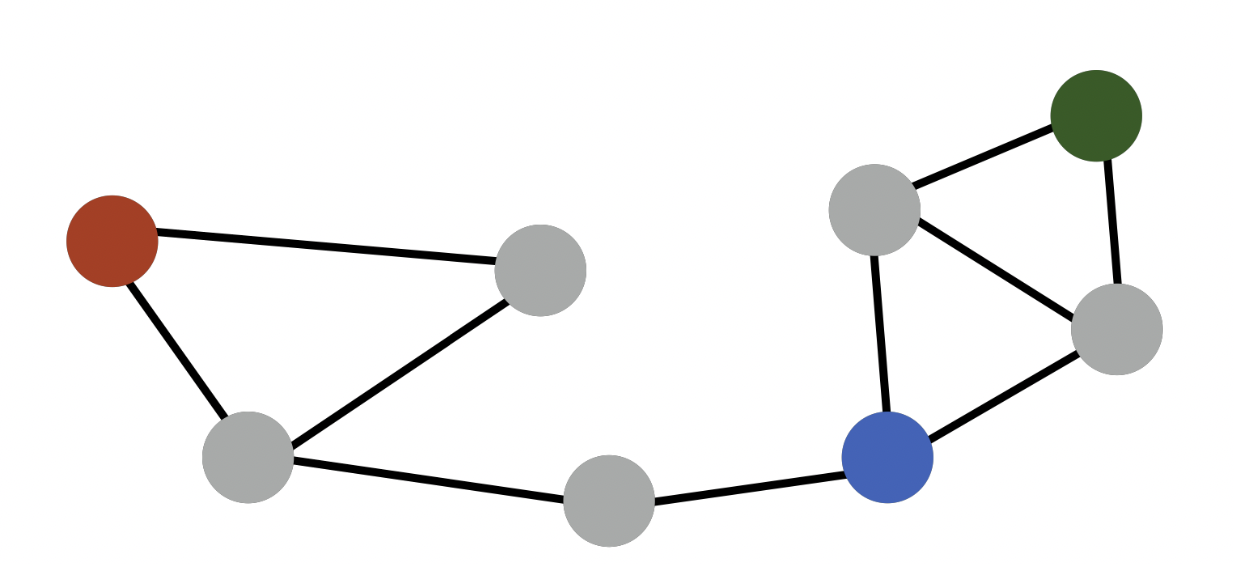
- 빨강-초록, 파랑-초록 인접성은 0 이지만 초록-파랑이 같은 군집에 속한다는 정보를 반영할 수 없음
거리/경로/중첩 기반 접근법
거리 기반 접근법
-
두 정점 사이의 거리가 충분히 가까운 경우 유사하다고 간주
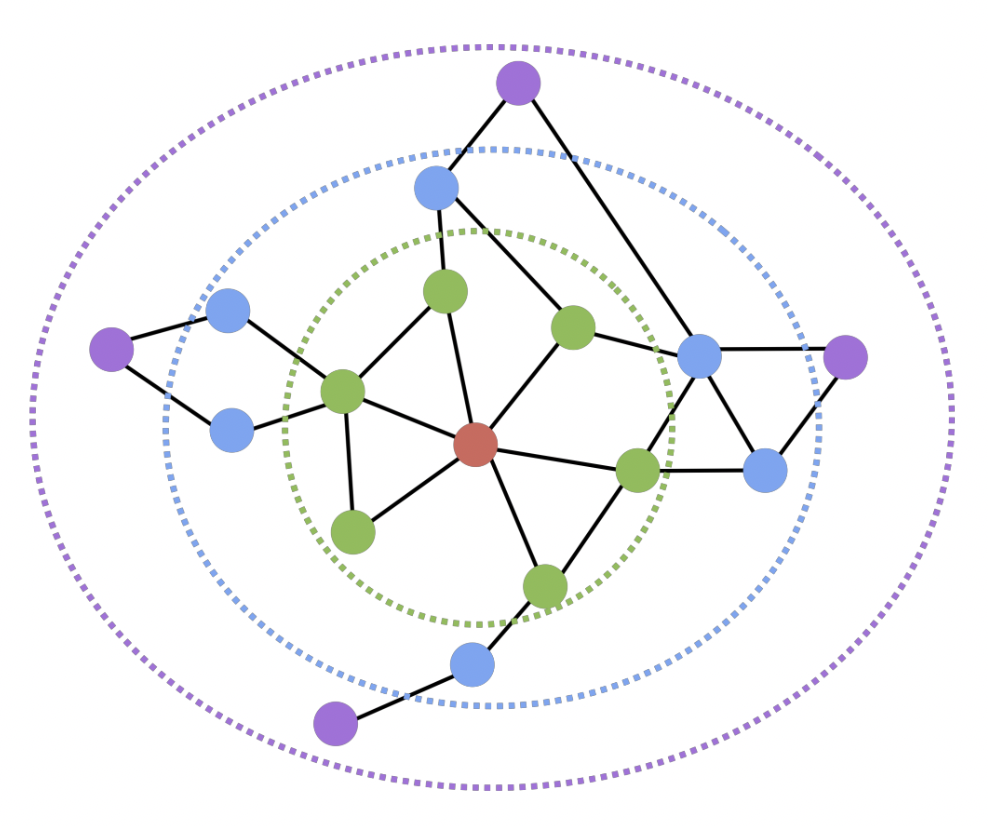
- 충분히의 기준을 거리 2 라고 가정해보자
- 빨강 기준, 초록과 파랑은 거리 2 안에 들어오므로 유사도 1 부여, 보라색은 유사도 0 부여
경로 기반 접근법
- 두 정점 사이의 경로가 많을 수록 유사하다고 간주
- 경로는 u 에서 시작해서 v 로 끝나고 순열에서 연속된 정점은 간선으로 연결됨을 만족하는 순열
-
$Ak_\mathit{u,v}$ : 경로 중 거리가 k 인것의 수
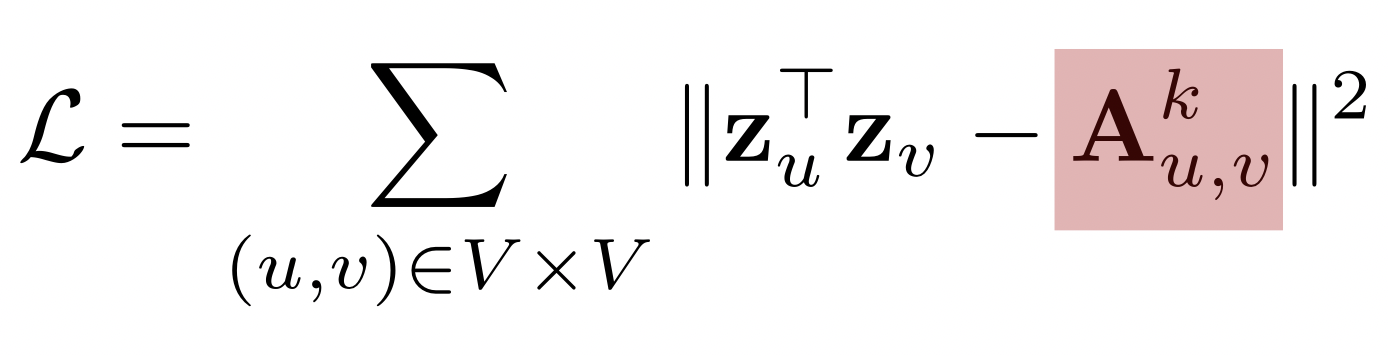
중첩 기반 접근법
-
두 정점이 많은 이웃을 공유할 수록 유사
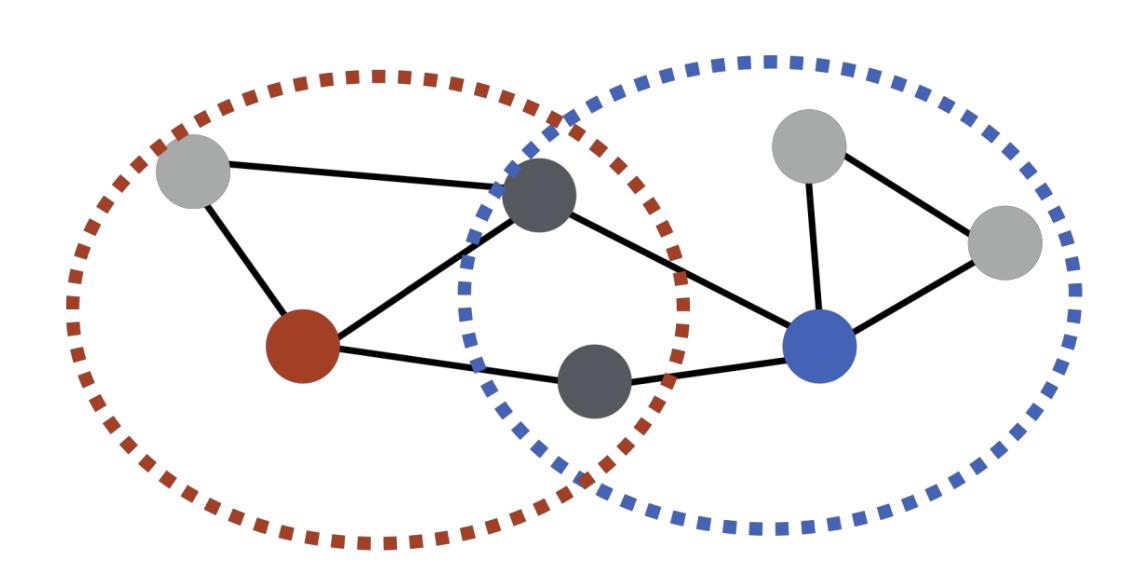
- 파랑과 빨강은 노드 2 개를 공유하므로 유사도 2

- 정점 u 의 이웃 집합 N(u)
-
공통 이웃 수 대신 자카드 유사도 or Adamic Adar 점수 사용 가능
- 자카드 유사도는 공통 이웃의 수 대신 비율을 계산
- N(u) 와 N(v) 의 교집합 / 이들의 합집합
- 0 ≤ 자카드 유사도 ≤ 1 (N(u) 와 N(v) 가 같으면 1)
-
Adamic Adar 는 공통 이웃 각각에 가중치를 부여하여 가중합 계산
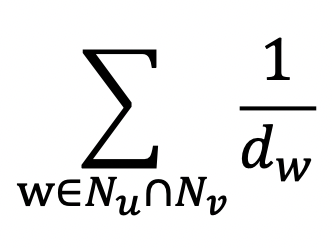
- 자카드 유사도는 공통 이웃의 수 대신 비율을 계산
임의보행 기반 접근법
임의보행 기반 접근법이랑
- 한 정점에서 시작하여 임의보행을 할 때 다른 정점에 도달할 확률을 유사도로 간주
- 임의보행은 현재 정점의 이웃 중 하나를 균일한 확률로 이동하는 반복 과정
- 임의보행은 시작 정점 주변의 지역적 정보와 그래프 전역 정보를 모두 고려한다는 장점이 있음
- 그래프 전역 정보 사용? 기존 방법들은 거리를 k 로 제한했지만 임의보행은 거리 제한 없음
- 과정
- 각 정점에서 시작하여 임의보행 반복 수행
- 각 정점에서 임의보행하여 도달한 정점들의 리스트 기록함. 정점 u 로부터 임의보행 중 도달한 정점들의 리스트는 $N_R(u)$ 라고 함. 한 정점을 여러 번 도달하면 해당 정점은 여러 번 포함됨
-
아래 로스 함수를 최소화하는 임베딩을 학습

- 어떻게 임베딩으로부터 도달 확률을 추정할까?
- P(v | $z_u$) 를 아래와 같이 추정
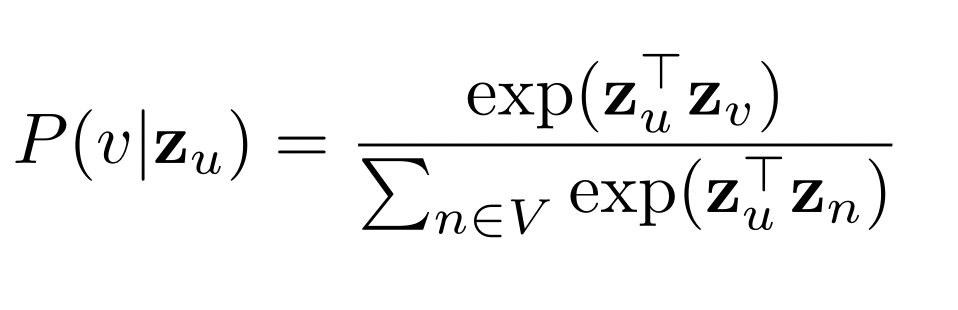
- 유사도 (내적) 이 높을 수록 도달 확률이 높음
-
추정한 도달 확률로 손실함수 재정의, 손실함수를 최소화하는 임베딩 학습

DeepWalk 와 Node2Vec
- 딥워크
- 앞서 설명한 기본적인 임의 보행
- 현재 정점의 이웃 중 하나를 균일한 확률로 반복 이동
- Node2Vec
- 2차 치우친 임의 보행 (Second-order Biased Random Walk) 사용
- 현재 정점 + 직전 정점 고려하여 다음 정점 선택
-
직전 정점의 거리를 기준으로 구분하여 차등적인 확률 부여, 부여하는 확률에 따라 다른 종류의 임베딩을 얻음
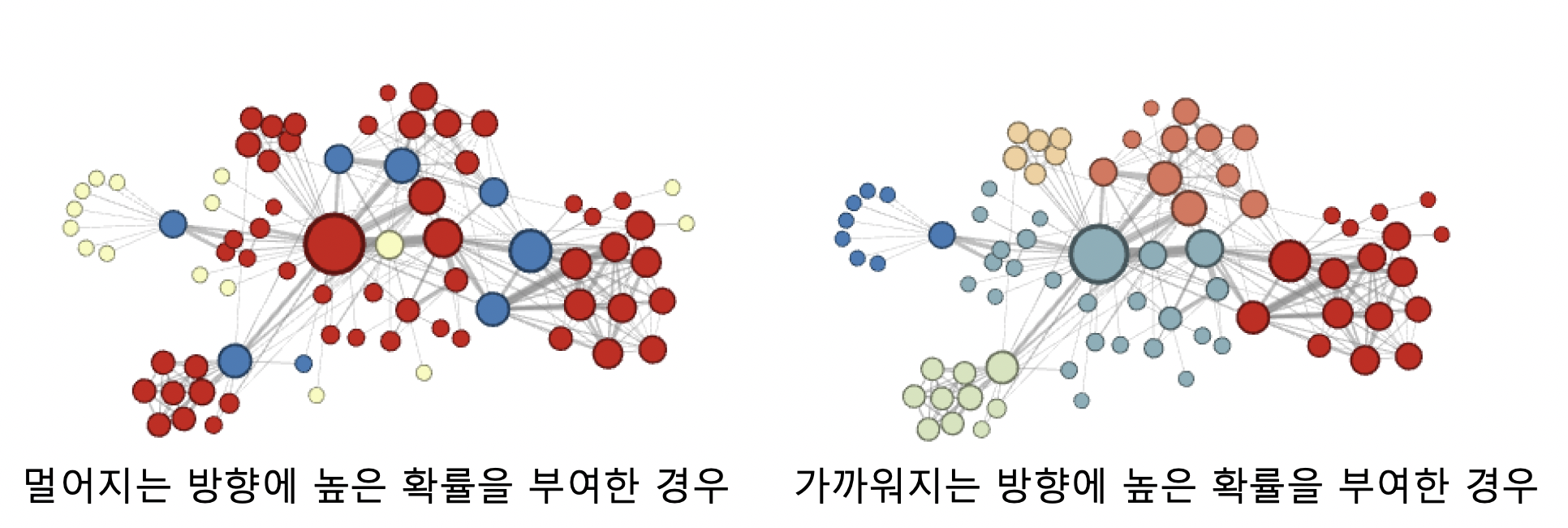
- 멀어지는 방향에 높은 확률 부여한 경우, 정점의 역할 (다리 역할, 변두리 정점 등) 이 같은 경우 임베딩 유사
- 가까워지는 방향에 높은 확률 부여한 경우, 같은 군집에 속한 경우 임베딩 유사
- 2차 치우친 임의 보행 (Second-order Biased Random Walk) 사용
손실 함수 근사
- 임의보행 기법의 손실함수는 계산 시간은 정점의 수 제곱 비례 (중첩된 합 때문)
- 정점이 많을 경우 시간 매우 오래 걸림
-
이를 막기 위해 근사식 사용, 모든 정점에 대해 정규화하는 대신 몇 개의 정점을 뽑아서 비교, 뽑힌 정점들을 네거티브 샘플이라 부름

- 연결성에 비례하는 확률로 네거티브 샘플로 뽑힐 확률 높아짐, 네거티브 샘플이 많을 수록 학습이 안정적
변환식 정점 표현 학습의 한계
변환식 정점 표현 방법과 귀납식 정점 표현 방법
- 변환식 정점 표현 방법
- 지금까지 본 정점 임베딩 방법들은 변환식 (Transductive) 방법
- 변환식 방법은 학습의 결과로 정점의 임베딩 자체를 얻는다는 특성이 있음
- 귀납식 정점 표현 방법
- 정점을 임베딩으로 변화시키는 함수, 인코더를 얻음
- 변환식 임베딩 방법의 한계
- 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩 불가능
- 모든 정점에 대한 임베딩 미리 계산해야함
- 정점의 속성 정보 활용 못 함
- 이러한 한계를 극복하기 위해 귀납식 임베딩 방법인 그래프 신경망 (GNN) 사용
군집 분석
- Girvan-Newman or Louvain 같이 군집을 찾아나서거나
- Node2Vec 으로 유사한 노드들을 임베딩해주고 K-Means 로 클러스터링해주거나
Further Reading
https://arxiv.org/pdf/1607.00653.pdf
https://arxiv.org/pdf/1403.6652.pdf
그래프를 추천시스템에 어떻게 활용할까? (심화)
넷플릭스 챌린지 소개
데이터셋
- 사용자별 영화 평점 데이터
- 트레이닝 데이터 : 2000~2005년까지 수집한 48만명 사용자의 1.8만개 영화에 대한 1억개 평점
- 테스트 데이터 : 각 사용자의 최신 평점 280만개
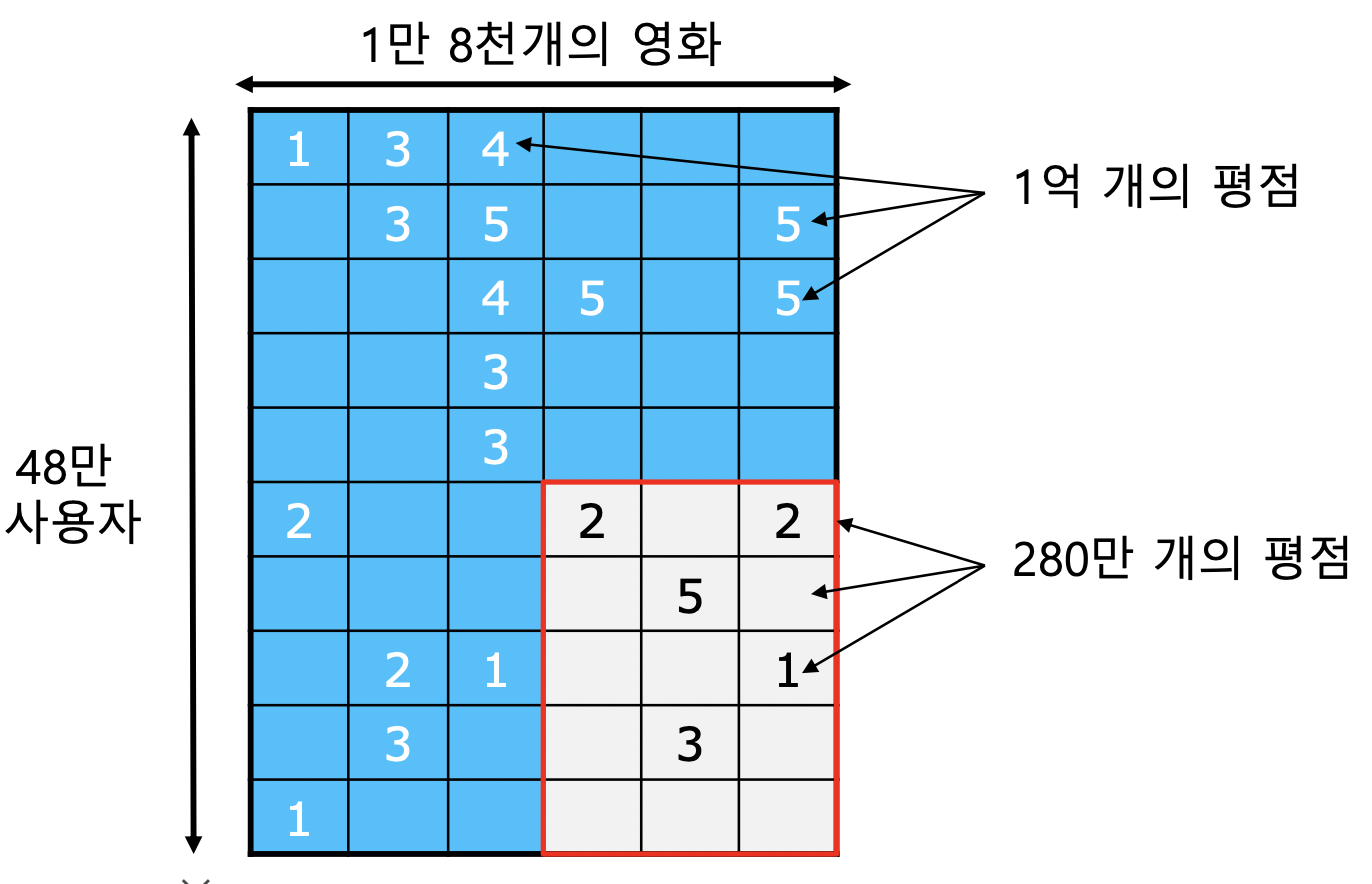
대회 목표
- 추천시스템 성능 10% 이상 향상
- MSE 를 0.9514 → 0.8563 까지 낮추면 100 만불 상금
- 2006~2009년 진행, 2700개 팀 참여, 추천시스템 성능 비약적으로 발전
-
성능

기본 잠재 인수 모형
개요
- 잠재 인수 모형 (Latent Factor Model, SVD 와 비슷하지만 다름) 의 핵심은 사용자와 상품을 벡터로 표현하는 것 (정점 표현 방법, 정점 임베딩)
- 사용자와 영화를 임베딩
-
고정된 인수 대신 효과적인 인수를 학습하는 것이 목표, 잠재 인수 = 학습한 인수
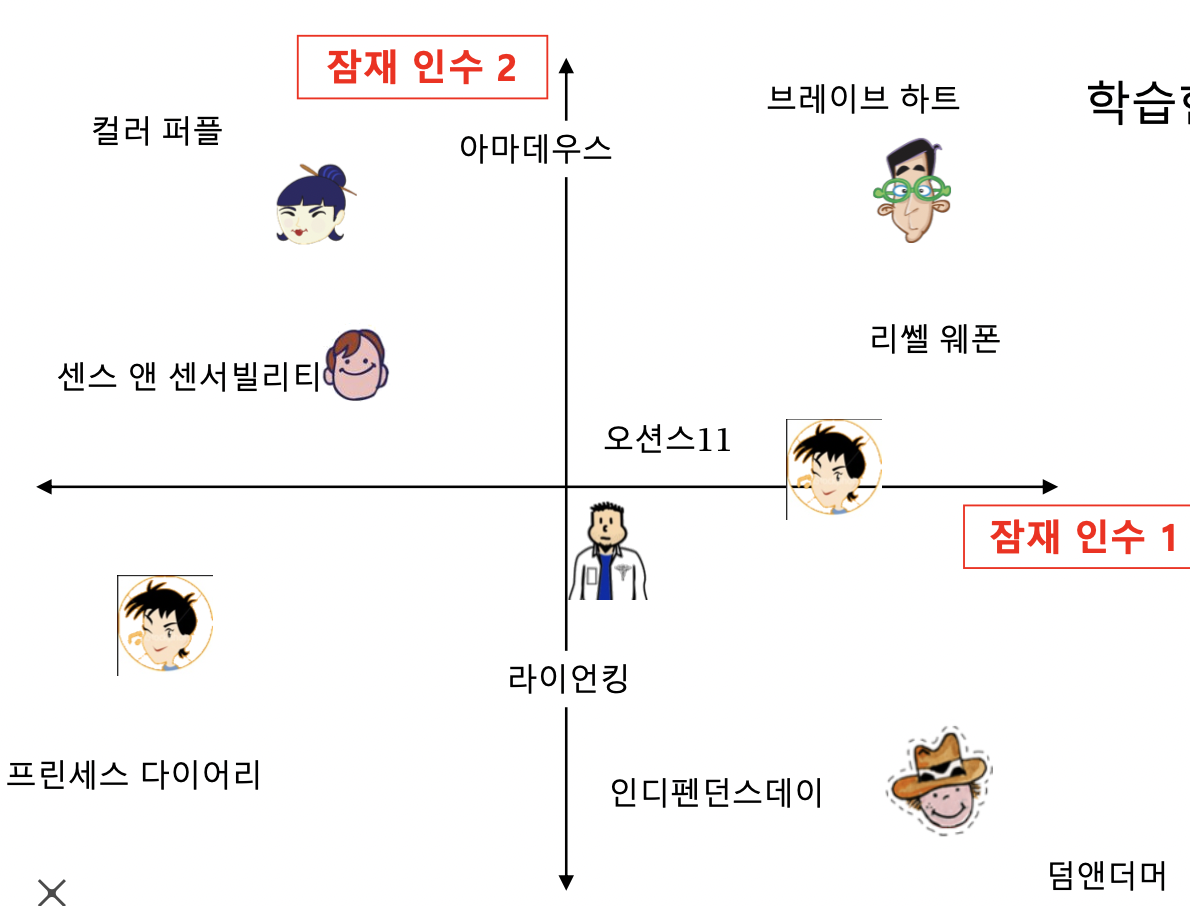
손실 함수
- 사용자와 상품을 임베딩하는 기준
- 사용자와 상품의 임베딩의 내적이 평점과 최대한 유사하도록 만듦
- 사용자 x 의 임베딩 $p_x$, 상품 i 의 임베딩 $q_i$, 사용자 x 의 상품 i 에 대한 평점 $r_\mathit{xi}$ 에 대해 pq 내적이 r 과 유사하도록 함
- 행렬 차원으로 보기
- 평점 행렬 R, 사용자 행렬 P, 상품 행렬 Q
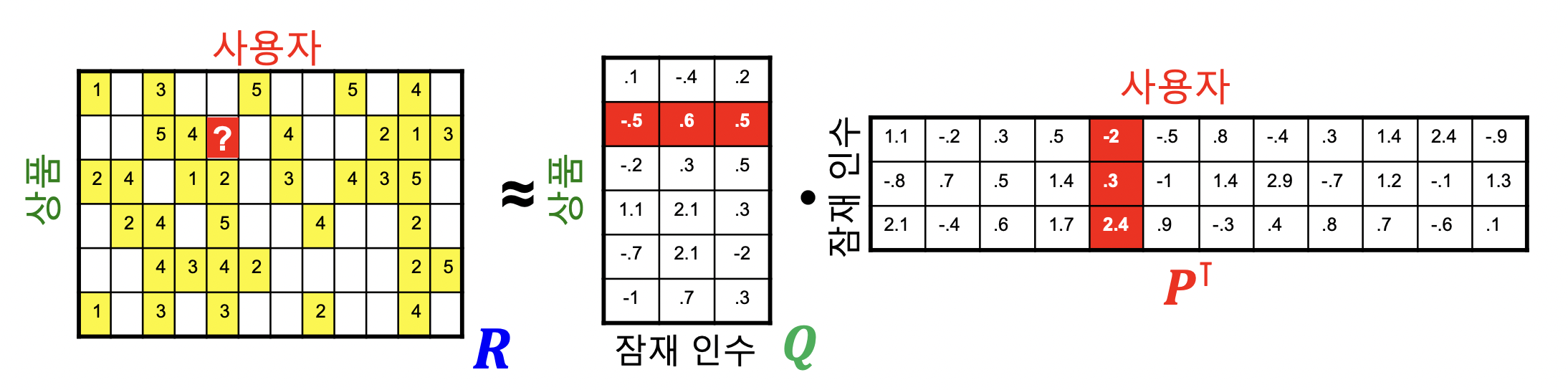
-
잠재 인수 모형은 아래 손실 함수를 최소화하는 P 와 Q 를 찾는 것을 목표로 함

- 위 손실 함수 사용할 시 오버피팅 (기계학습 모형이 훈련 데이터의 잡음까지 학습하여 테스트 성능 떨어지는 경우) 발생 가능
-
과적합을 방지하기 위해 정규화 항을 손실 함수에 더함 (L-2 Regularization 항 추가)

- 오차도 줄이고 모형 복잡도도 줄여야 함
- 임베딩이 너무 크면 잡음까지 배울 수 있기 때문에 임베딩을 줄여줌
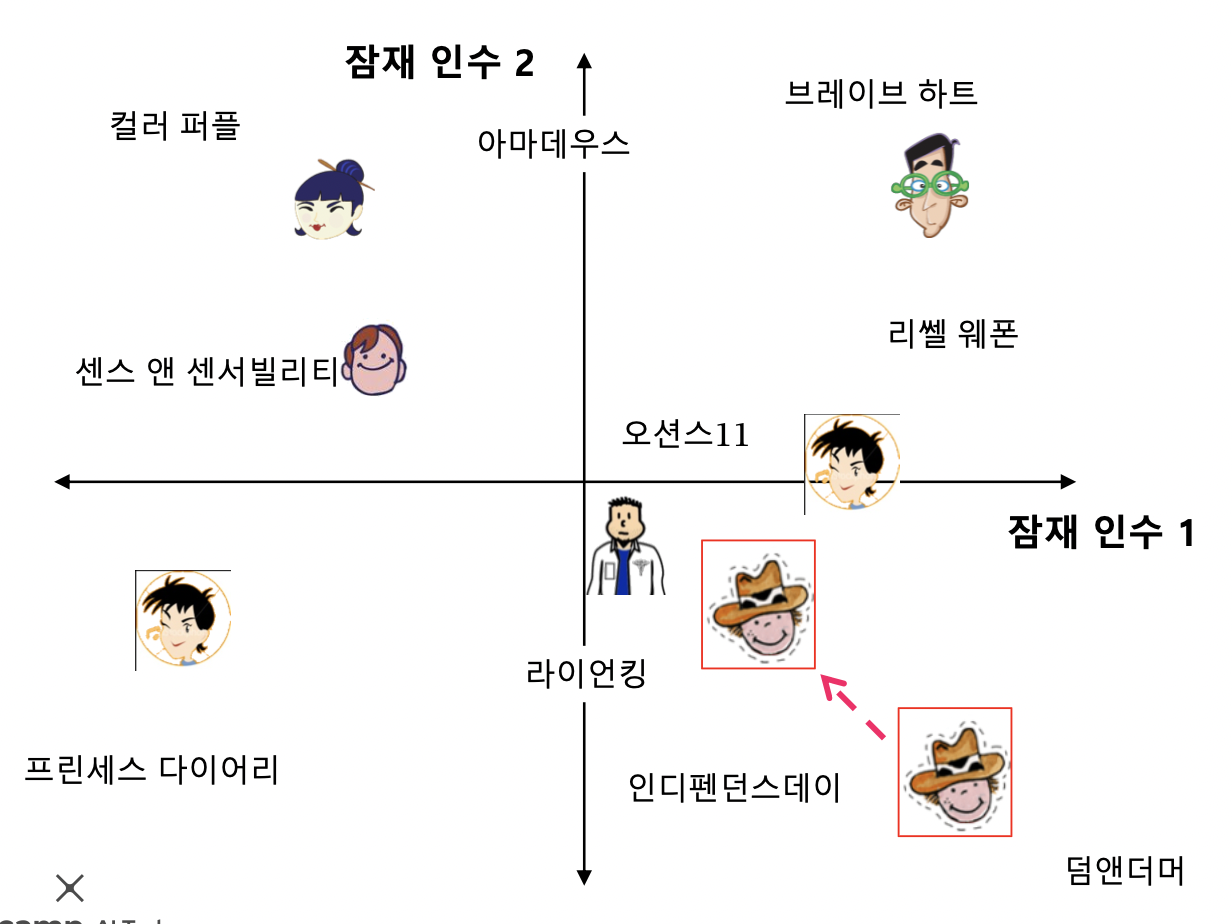
- 위 사진과 같이 정규화는 너무 큰 임베딩을 방지
최적화
- 손실함수를 최소화하는 P, Q 를 찾기 위해 (확률적) 경사하강법, SGD 사용
- 경사하강법은 손실함수를 안정적으로 변화시키지만 느리고 로컬 미니멈에 빠질 수 있음
- SGD 는 불안정하게 변화시키지만 빠르게 감소시키고 미니멈에서 나올 가능성을 높여줌 (덜 신중하게 걸음을 해서 빠르게 이동)
결과
- 기본 잠재 인수 모형 사용 MSE : 0.9
고급 잠재 인수 모형
사용자와 상품의 편향을 고려한 잠재 인수 모형
- 사용자의 편향은 해당 사용자의 평점 평균과 전체 평점 평균의 차
- A 의 평점 평균 4.0, B 의 평점 평균 3.5, 모든 사람의 평점 평균 3.7 이면 A 의 사용자 편향은 4-3.7 = 0.3, B 의 사용자 편향은 3.5-3.7 = -0.2
- 상품의 편향은 해당 상품에 대한 평점 평균과 전체 평점 평균의 차
- 영화 a 의 평점 평균 4.5, b 의 평점 평균 3.0, 전체 영화 평점 평균 3.7 → a 상품 편향 : 0.8, b 상품 편향 : -0.7
-
개선된 잠재 인수 모형은 전체 평균, 사용자 편향, 상품 편향, 상호작용으로 분리

- 예전에는 상호작용만 고려한 것에 비해 개선됨
-
손실 함수
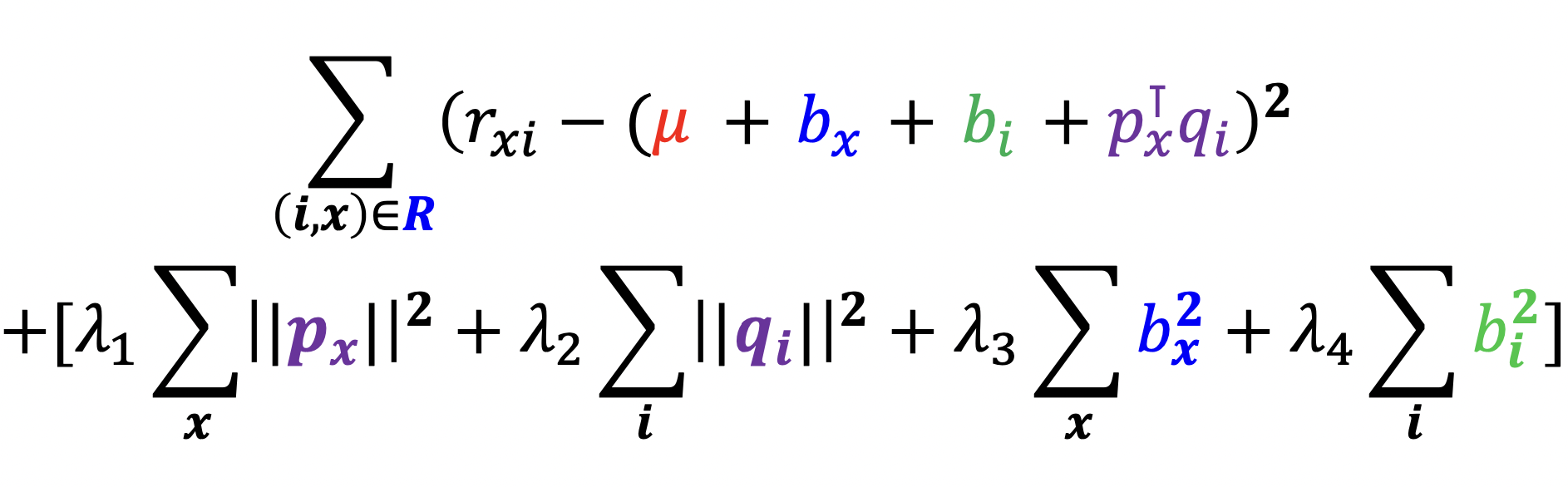
- 결과
- 사용자와 상품의 편향을 고려한 잠재 인수 모형 MSE : 0.89
시간에 따른 편향을 고려한 잠재 인수 모형
-
넷플릭스 시스템 (UI 등) 의 변화로 그 이후 평점이 크게 상승하는 사건이 있었음 (전체 영화)
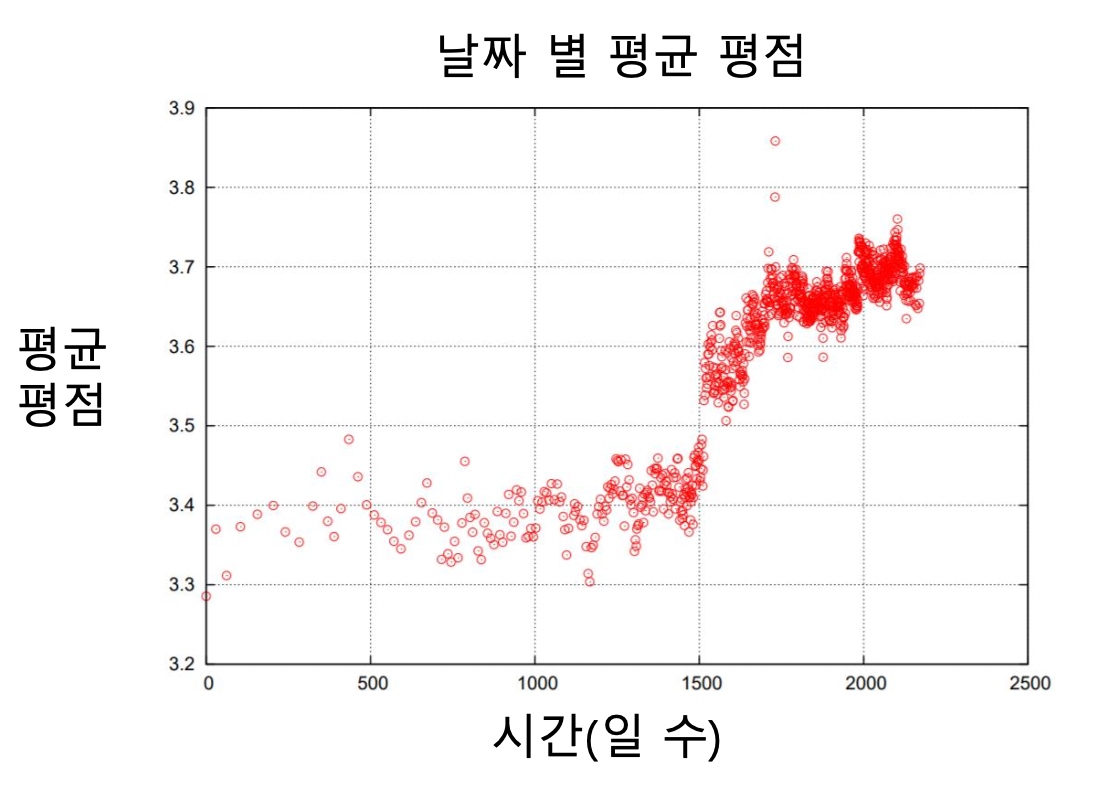
-
영화의 평점은 출시일 이후 시간이 지남에 따라 상승하는 경향이 있음 (각 영화)
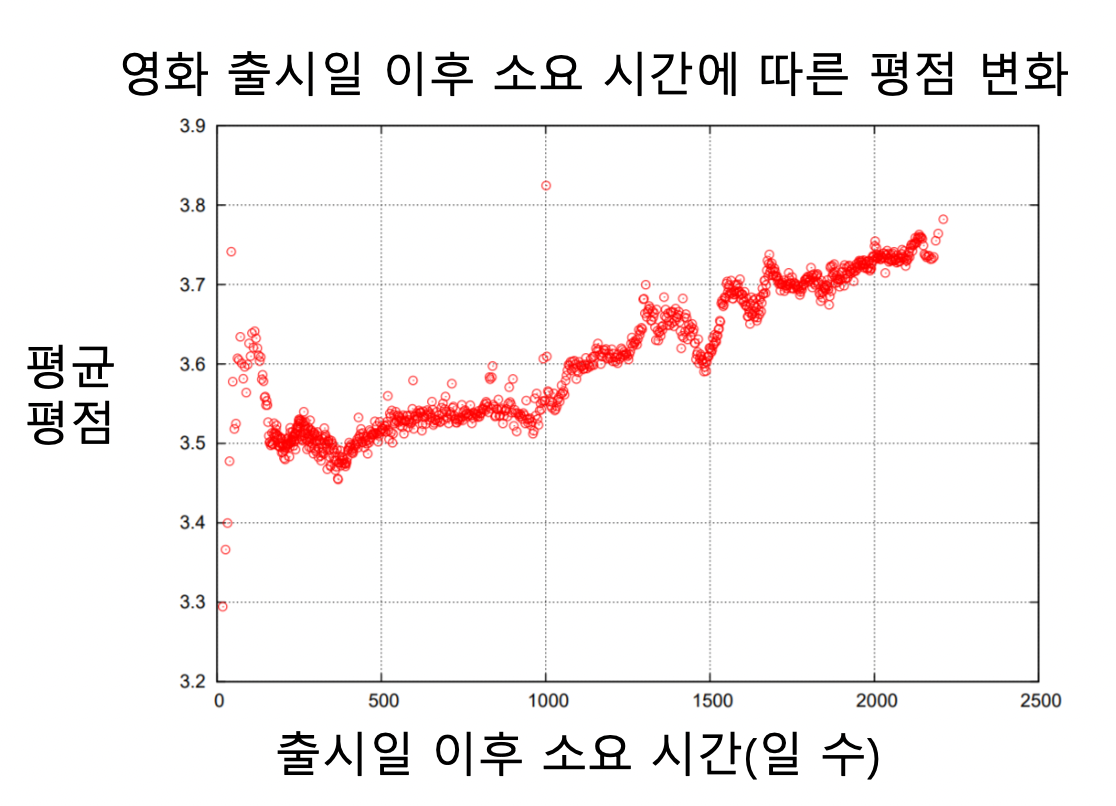
- 처음 높은건 영화를 기다리는 사람들
- 떨어지는건 다른 사람들
- 다시 올라가는건 추천받거나 찾아서 본 사람들
-
시간적 편향을 고려한 잠재 인수 모형

- 사용자 편향과 상품 편향을 시간에 따른 함수로 가정
-
결과
- 시간에 따른 편향을 고려한 잠재 인수 모형 MSE : 0.876
넷플릭스 챌린지 결과
앙상블 학습
- 개선된 잠재 인수 모형으로 거의 목표 오차 다와감
- BelKor 팀이 앙상블을 사용해서 목표 오차 달성
- 다른 팀들이 연합해서 앙상블하여 목표 오차 달성
- 두 팀 오차 정확히 일치 (먼저 20분 먼저 도달한 BelKor 팀 우승)
Further Reading
- http://infolab.stanford.edu/~ullman/mmds/ch9.pdf
- https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf
Further Questions
- 추천시스템의 성능을 측정하는 metric이 RMSE라는 것은 예상 평점이 높은 상품과 낮은 상품에 동일한 페널티를 부여한다는 것을 뜻합니다. 하지만 실제로 추천시스템에서는 내가 좋아할 것 같은 상품을 추천해주는것, 즉 예상 평점이 높은 상품을 잘 맞추는것이 중요합니다. 이를 고려하여 성능을 측정하기 위해서는 어떻게 해야 할까요?
- 추천 시스템의 성능을 향상시키기 위해서는 어떠한 것을 더 고려할 수 있을까요? (해당 문제는 정답이 제공되지 않는 문제입니다. 자유롭게 여러분의 의견을 이야기해보세요.)
피어 세션
수업 질문
[펭귄] Louvain 알고리즘이 군집을 형성하는 과정
Today I Felt
ByeBye MJ
취업으로 MJ님의 피어세션은 오늘이 마지막이었다. 짧아 보이는 5주라는 시간동안 온라인으로만 봤지만 공부하면서 힘이 되고 도움도 많이 받았기 때문일까, 내일부터 같이 못한다고 생각하니 많이 아쉽다. 하지만 좋은 일로 보내드리는거니 앞으로의 날에 좋은 일만 있길 기원한다. 그리고 U 스테이지 자체도 이제 2주 정도 밖에 남지 않았는데 남은 기간 조원들과 소통하며 더 성장하고 좋은 마무리를 할 수 있도록 노력해야겠다.