시각화 도구

우리가 사용하려는 데이터는 어떻게 생겼는지 보여주는 도구
데이터 시각화를 못하면 데이터 분석 못한다고 말씀

matplotlib

pyplot 객체를 사용하여 데이터를 표시
pyplot 객체에 그래프들을 쌓은 후 flush(show함수) (보여주고 나면 비움)
Graph 는 기본 figure 객체에 생성됨
pyplot 객체 사용시 기본 figure 에 그래프가 그려짐
plot 은 라인 그래프이므로 쌍 안맞추면 이상하게 그려짐 → X 순서대로 Y 값 적을 것
plot 만 해도 그려지긴 함, 그래도 show 쓰자

import matplotlib.pyplot as plt

X = range(100)
Y = range(100)
plt.plot(X,Y)
plt.show()

결과

Figure & Axes

기본 figure 객체 외에 따로 객체를 저장해서 사용 가능
subplot 은 grid 구조로 할당 가능

fig = plt.figure() # figure 반환
fig.set_size_inches(10,3) # 크기지정
ax_1 = fig.add_subplot(1,2,1) # 두개의 plot 생성
ax_2 = fig.add_subplot(1,2,2)  # 두개의 plot 생성

ax_1.plot(X_1, Y_1, c="b")  # 첫번째 plot
ax_2.plot(X_2, Y_2, c="g")  # 두번째 plot
plt.show() # show & flush

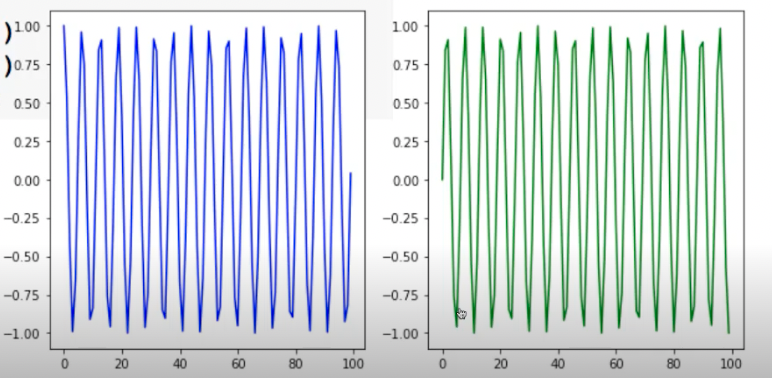
여러 속성들

Set color
- plot 의 속성으로 c or color 설정 가능, rgb 나 영소문자 심벌 사용가능

X_1 = range(100)
Y_1 = [value for value in X]

X_2 = range(100)
Y_2 = [value + 100 for value in X]

plt.plot(X_1, Y_1, color="#000000")
plt.plot(X_2, Y_2, c="c")

plt.show()

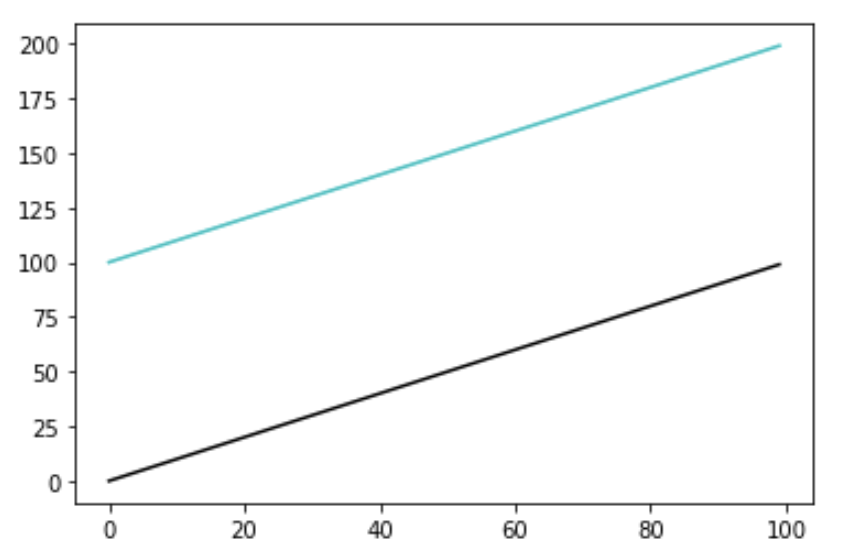
Set linestyle
- ls or linestyle 속성 설정
Set title
- latex 타입의 표현도 가능 (수식 표현 가능)
- plt.title(‘tt’)
Set legend
- 범례 표시 가능
text 나 annotation 도 설정 가능
저장
- savefigure 사용
- show (flush) 전에 해줘야 함

scatter

산전도 그리는 함수
marker 는 scatter 모양 설정
다 검색해서 쓰면 됨

bar

막대 그래프 그려주는 함수
가로 형태의 hbar 함수도 있음

histogram

분포차트 그려주는 함수
hist 함수 사용, bins 속성 개수만큼 칸을 나눔

boxplot

알아둘 필요 있음 (박스플롯 자체 의미도)
- 데이터에 대한 분포를 박스 형태로 그려줌, 몰린 정도와 범위까지 (아웃라이어도)
boxplot 함수 사용

seaborn

statistical data visualization (통계적 데이터 시각화)
matplotlib 를 더 쉽게 다루도록 도와줌 (matplotlib 의 wrapper)
기존 matplotlib 에 기본 설정을 추가
복잡한 그래프를 간단하게 만들 수 있는 wrapper
간단한 코드 + 예쁜 결과
load_dataset 할 때 “tips” 와 “fmri” 많이 씀 (기본 데이터셋)
import seaborn as sns 로 함

basic plot

lineplot
- 주 데이터 선과 분포가 위아래로 나옴
- hue 속성에 카테고리를 넣으면 카테고리 별로 나눠줌

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")
tips = sns.load_dataset("tips")
fmri = sns.load_dataset("fmri")
sns.set_style("whitegrid")
sns.lineplot(x="timepoint", y="signal", data=fmri)

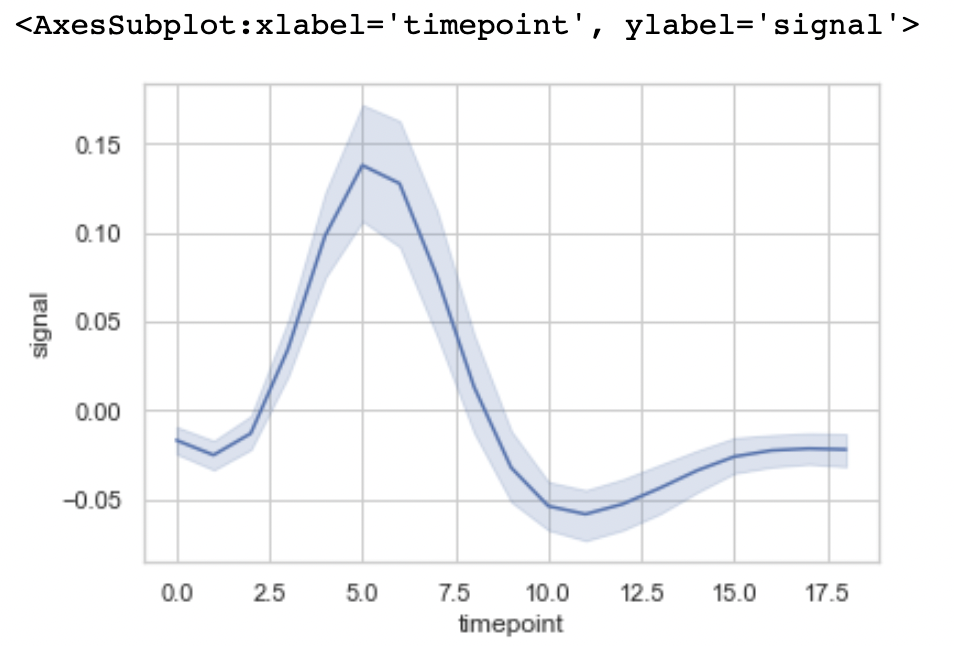
scatterplot
- 기본 scatter 와 거의 동일
- hue 사용 가능
regplot
- scatterplot 에다가 regression line (선형회귀선) 도 그려줌
countplot
- 카테고리 데이터를 위해 쓰고 카테고리 데이터 개수를 세어줌
barplot
- 막대 그래프 그려줌
distplot
- 데이터의 분포를 그려줌
violinplot
- 바이올린 플롯 (일반적으로 많이 사용), 분포 보기 편함
swarmplot
- 데이터 적을 때 괜찮음, 분포 보기 편함
기타 여러 플롯 많음

통계학 맛보기

모수가 뭐에요?

통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표
유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아내는 것은 불가능 → 근사적으로 확률분포 추정
- 예측모형의 목적은 분포를 정확하게 맞추는 것보다는 데이터와 추정 방법의 불확실성을 고려해서 위험 최소화하는 것
데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter) 를 추정하는 방법이 모수적(parametric) 방법론
특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수적(nonparametric) 방법론이라 부름
- 기계학습의 많은 방법론은 비모수 방법론에 속함
- 모수가 없는게 아니라 모수가 무한히 많거나 데이터에 따라 바뀌는 것

확률분포 가정 예제

확률분포를 가정하는 방법 : 우선 히스토그램을 통해 모양 관찰
- 데이터가 2개의 값 (0, 1) 만 가지는 경우 → 베르누이 분포
- 데이터가 n 개의 이산적인 값을 가지는 경우 → 카테고리 분포
- 데이터가 [0, 1] 사이에서 값을 가지는 분포 → 베타분포
- 데이터가 0 이상의 값을 가지는 경우 → 감마분포, 로그정규분포 등
- 데이터가 $R$ (실수) 전체에서 값을 가지는 경우 → 정규분포, 라플라스분포 등
→ 연속확률분포와 이산확률분포를 관찰되는 분포에 따라 결정할 수 있음
기계적으로 확률분포를 가정 x, 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙 (데이터를 관찰하고 선택해야함)

→ 어떤 확률분포로 모델링했을 때 모수 추정과 더불어 반드시 각 분포에 적절한 방법으로 검정을 해야함

데이터로 모수 추정하기

데이터의 확률분포를 가정했으면 모수 추정 가능
정규분포의 모수는 평균 $\mu$ 와 분산 $\sigma^2$ 를 사용하고 이를 추정하는 통계량(statistic) 은 다음과 같음 (모집단의 평균은 $\overline{X}$, 분산은 $S$)
- 표본 평균 : 산술평균 → 전체 데이터 평균 기대값 $E[\overline{X}] = \mu$
- 표본 분산 : (데이터 - 모평균)^2 의 산술평균 → $E[S^2] = \sigma^2$
통계량의 확률분포를 표집분포(sampling distribution) 라 부르며, 특히 표본 평균의 표집분포는 N 이 커질수록 정규분포 $N(\mu,\ \sigma^2/N)$ 을 따름
- 이것이 중심극한정리 (모집단의 분포가 정규분포를 따르지 않아도 성립)
  - 분포에서 추출한 통계량, 표본평균의 데이터가 많을수록 분산은 0 에 가까워지고 가운데 (평균) 으로 몰림

최대가능도 추정법

표본평균이나 표본분산은 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라짐
이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법 (maximum likelihood estimation, MLE)
- 가능도 함수 $L(\theta;\ x)$ : 주어진 데이터 x 에 대해 모수 세타를 변수로 둔 함수, 즉 데이터가 주어진 상태에서 세타를 변형시킴에 따라 값이 바뀌는 함수. 모수 세타를 따르는 분포가 데이터 x 를 관찰할 가능성 (다 더해서 1 이 안되므로 확률로 해석하면 안됨)
데이터 집합 X 가 독립적으로 추출되었을 경우 로그가능도를 최적화함
- 로그 씌우고 덧셈식으로 최적화 가능
  - 독립 표본 : 서로 다른 항목의 집합에서 얻은 측정값
  - 종속 표본 : 한 항목의 집합에서 얻은 측정값
왜 로그가능도 사용하는가?
- 로그가능도를 최적화하는 모수 세타는 가능도를 최적화하는 MLE
- 데이터의 숫자가 적으면 상관없지만 만일 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로는 가능도 계산 불가능
- 데이터가 독립이면 로그를 통해 가능도의 곱셈을 덧셈으로 바꿀 수 있음 → 컴퓨터로 연산 가능
- 경사하강법으로 가능도 최적화할 때 미분 연산을 하는데, 로그 가능도를 사용하면 이 연산량을 O($n^2$) 에서 O(n) 으로 줄여줌
- 대게의 손실함수의 경우 경사하강법을 사용하므로 음의 로그가능도를 최적화

최대가능도 추정법 예제 : 정규분포

정규분포를 따르는 확률변수 X 로부터 독립적인 표본 {x1, …, xn} 을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
- 주어진 데이터를 가지고 (로그) likelihood 를 최적화하는 세타를 찾아야 함
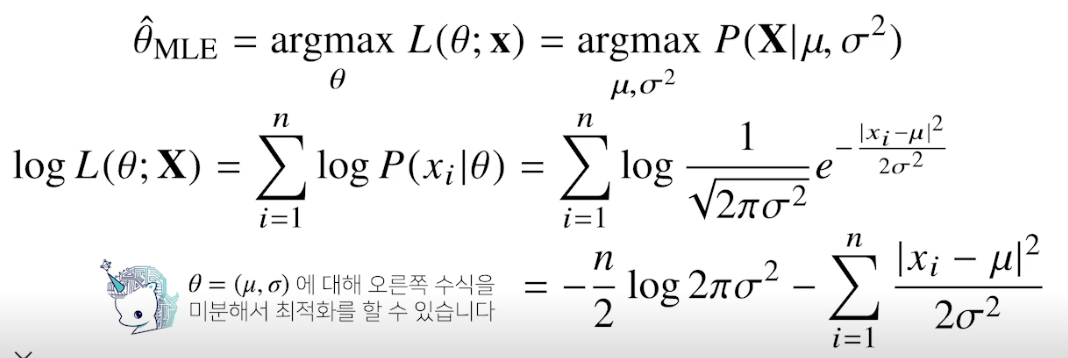
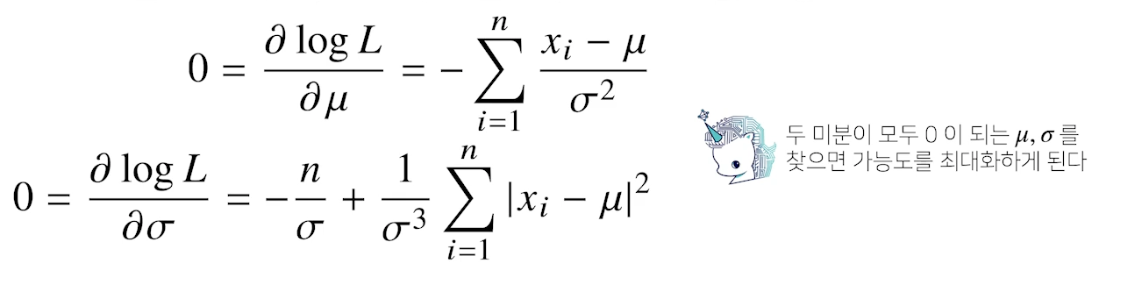
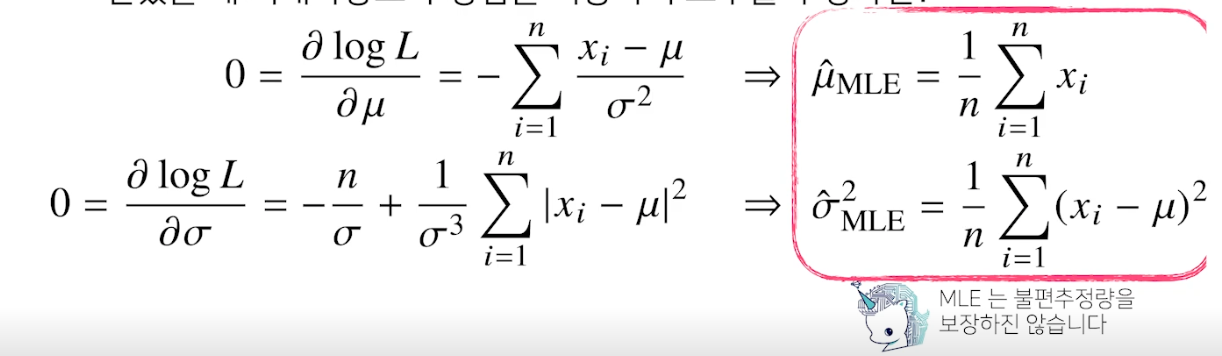
- 불편추정량을 보장하진 않지만 consistence 는 보장

최대가능도 추정법 예제 : 카테고리 분포

카테고리 분포 Multonoulli(x; p1, …, pd) 를 따르는 확률변수 X 로부터 독립적인 표본 {x1, …, xn} 까지 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?

(정규분포의 모수는 평균과 분산이라는 통계량인 반면, 카테고리 분포의 p 들은 1~d 차원까지 각각의 차원에서 값이 1 또는 0 이 될 확률을 의미하는 모수 → p1 ~ pd 다 더하면 1)

(Q. MLE 식에 대한 정확한 뜻을 모르겠음 → 원딜님 피피티 다시보자)

딥러닝에서 최대가능도 추정법

기계학습 모델 학습에서 사용
딥러닝 모델의 가중치를 $\theta$ = (W(1) , …, W(L)) 이라 표기했을 때 분류 문제에서 소프트맥스 벡터는 카테고리분포의 모수 (p1, …, pk) 를 모델링함
원핫벡터로 표현한 정답레이블 y = (y1, …, yk) 를 관찰 데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도 최적화 가능

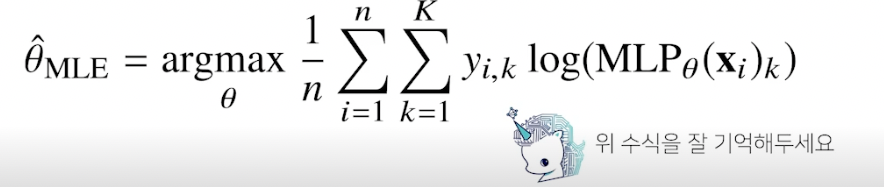
확률분포의 거리 구하기

기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도
데이터공간에 두 개의 확률분포 P(x), Q(x) 가 있을 경우 두 확률분포 사이의 거리를 계산할 때 다음과 같은 함수들을 이용
- 총변동 거리 (Total Variation Distance, TV)
- 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)
- 바슈타인 거리 (Wasserstein Distance)

쿨백-라이블러 발산

정의
- 뒷 자리 Q 를 로그의 분모로 앞자리 P 를 로그의 분자로
- 이산은 시그마, 연속은 적분
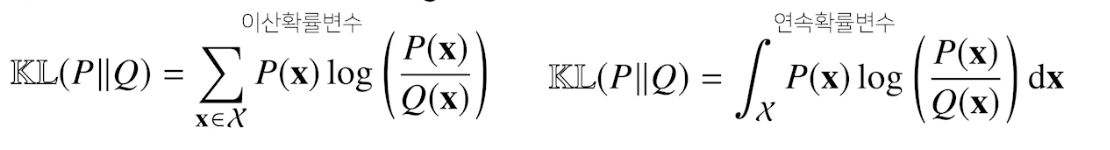
분해
- 두 개의 엔트로피 표현 가능
분류 문제에서 정답레이블을 P, 모델 예측을 Q 라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화하는 것과 같음
- 기계학습의 원리는 데이터로부터 확률분포 사이의 거리를 최소화하는 것과 동일

Further Question

확률과 가능도의 차이는 무엇일까요? (개념적인 차이, 수식에서의 차이, 확률밀도함수에서의 차이)
확률 대신 가능도를 사용하였을 때의 이점은 어떤 것이 있을까요?
다음의 code snippet은 어떤 확률분포를 나타내는 것일까요? 해당 확률분포에서 변수 theta가 의미할 수 있는 것은 무엇이 있을까요?

피어 세션

질문

표본분산에서 n-1 인 이유

모집단의 표준편차와 비슷하게 만들기 위해 보정한 것
엔트로피

데이터를 나눠주는 기준, 디시전 트리에서 가장 빠르게 분류할 수 있게 만들어주는 손실함수로 크로스 엔트로피가 사용됨

펭귄님 : Further Question 은 피어세션에서 다루자.

마스터 클래스

1. AI 관련해서 추천 해주실만한 책이 있나요?

영어책 괜찮으면 아마존 ‘Dive into Deep Learning (D2L)’
- 코드랑 수식 다 있어서 좋음
- PRML 등 좋은 책 많지만 코드 관련은 적어서 이 책 추천
한글책은 ‘밑바닥부터 시작하는 딥러닝’

2. AI 를 공부하면서 수학의 중요성을 느끼는데 확률, 통계, 선대 공부 어떤식으로 할까요?

코드랑 같이 공부하는거 추천! 수식을 코드로 어떻게 쓰는지 같이 보는게 가장 중요 → D2L 책 좋음

3. 강화학습은 목적함수 설정이 어려움, 복잡한 태스크의 목적 함수는 수학자를 통해 나오는지 아니면 거듭된 수정을 거치는지 궁금합니다.

수학자가 하다 망한 경우 많음, 수학자가 하지 않음
엔지니어들이 문제를 쪼개면서 설계해서 만든 경우가 더 많음
디버깅이 더 중요
원하는 목적에 맞는 더 효율적인 수식을 짤 때 수학자 필요, 보통은 더 간단함

4. 여러 모델들의 수학적 원리를 다 이해해야 할까요? 수학적 수식이 실제로 일할 때 어떻게 쓰이는지 궁금합니다.

모든 걸 다 이해하면 좋지만 그 때 그 때 찾아서 씀
영어로 비유하면 모르는 단어는 사전 찾아보듯 함, 대신 알파벳처럼 기본적은 알아야 함
현업에서는 수식부터 먼저 이해하고 코딩 시작함

5. 추천시스템 및 AI 금융 트레이딩을 위해 알아야할 선행 지식이 있을까요?

추천시스템을 위해 선형대수 지식 필요하고 베이즈 정리 등도 필요함.
금융 트레이딩에서는 광범위하지만 단적으로는 금융 시스템은 확률 기반이라 확률론이라는 통계적 지식 등이 많이 필요함, 강화학습을 위해 더 심화된 선대, 확률론 등 내용 필요

6. ML/DL 리서쳐가 아닌 엔지니어는 수학을 어느정도 알아야 할까요?

본인 업무에 필요한 정도
보통 리서쳐와 엔지니어는 수학 좋아하고 잘 함. 직접 공부하고 모르는 부분을 채워나가야 함. 이정도만 알면 되겠지가 아니라 필요한거 그때그때 공부해야함. 이것을 위한 수학에서의 기초 체력이 필요함.

7. 강화학습이 현업에서 적용되고 있나요?

몇몇 우리가 알만한 회사에서는 교통 관련 시스템 통제나 추천 시스템 만들 때 강화학습 사용중
수학을 엄청 쓰기보다는 하드코어한 엔지니어링으로 해결 많이 함

8. 교수님이 부스트캠프 수강생이라면 어떤 공부를 중점적으로 하실 것 같으신가요?

코드랑 수학이랑 매칭하면서 공부할 것
그렇다고 너무 코드만 집중하면 깊이가 떨어짐. 아이디어에 대해 다른 사람에게 의존하게됨.
수학은 새로운 아이디어 떠올릴 때 좋고 코드는 아이디어를 구현할 수 있어서 좋음
리서쳐 : 수식 ↔ 코드 매칭 둘 다 해야함
엔지니어 : 수식 → 코드 매칭 훈련 필요
다이브 인 투 딥러닝 꼭 해라! 그 책 코드 모든 부분 따라하면서 공부할 것

9. 수학이 많이 어려운데 강의 내용을 더 자세히 볼 수 있는 책이나 강의가 있을까요?

PRLM 책?
이번 강의는 여러 키워드를 던져주고 직접 구글링해서 찾아보는 식으로 공부 추천
구글링도 추천

라이브 Q&A

1. 인공지능 관련으로 공부하고 취업하려면 대학원은 필수일까요? 입학하기 위해서는 어떤 준비를 해야할까요?

필수는 아님, 하지만 도움이 많이됨
모르는 부분을 대학원에서 해소할 수 있어서 좋음
딥러닝 인공지능 분야는 매우 넓기 때문에 대학원에서 지도 받으면서 전문적으로 컨설팅 받으면서 클 수 있어서 좋다.
입학 준비
- 컴공 지식, 머신러닝 지식 (이번 부캠에서 배운 내용 정확히 알면 충분), 더 깊이는 알고리즘 공부해도 좋음.
- 임교수님 랩 선발 기준은 메일 보내면 답해주겠다.

2. 딥러닝에서 기존 변수를 결합해 파생변수를 만드는것(피쳐엔지니어링)이 결과에 도움이 되나요? 기존 변수를 선형결합하거나, 나누거나 곱해 새로운 변수를 만드는데 모델에 어떤 영향을 주는지 궁금합니다.

진리의 케바케임
근데 지식을 갈아넣는 피쳐엔지니어링보다는 데이터 부분 (원하는 퍼포먼스를 위해 이 데이터가 도움되는가, 데이터 전처리 등) 이 더 도움되었음.

3. 통계학 공부 책 추천

통계 이론 공부하고 싶다면 PRML, 통계학 도감 등 (수식보다 직관적으로, 그림으로 이해되는 경우가 더 많음)

4. 시계열 데이터를 다룰 때 데이터의 시기(t) 에 의해 모델이 오버피팅 될 수 있는데 예를 들면 과거 데이터에 너무 편향된 경우, 이럴 때는 어떻게 해결하나요?

모델마다 다름.
RNN은 반대로 최근 데이터에 너무 집착하는 걸 잡으려고 LSTM 을 사용하기도 했음

5. 딥러닝을 확률론적으로 접근하는 것과 백프로파게이션을 통해서 딥러닝을 하는 것과 다른 관점인가요? 제가 생각하기엔 백프로파게이션을 통해 학습을 하는 점에서는 확률과 통계학이 사용되지 않는 것 같은데 확률과 통계는 다른 관점에서 접근하나요?

백프로파게이션은 싱글 데이터에서 진행되는데, 전체 데이터에 대해 미니배치로 학습하고 확률적으로 접근하기 떄문에 사용. 드롭아웃 등도 통계나 확률에서 사용되는거 많음
다른 관점이 아니라 백프로파게이션뿐만 아니라 확률과 통계라는 기법도 사용할 수 있음.

6. 엔지니어링이란?

이론적으로 풀려는건 리서쳐적인 태도
직관이나 문제해결 측면으로 보는게 엔지니어링 태도
하드웨어나 소프트웨어 발전으로 문제가 해결되는 경우도 많음 → 엔지니어링 영역

교수님 말씀

수학 공부도 운동과 비슷함, 수업에 그치지 않고 계속 찾아보고 공부하는 습관 들이면 필요한 것을 찾아서 사용하는데 용이함
기초를 다 공부하고 머신러닝을 공부하는거보다, 어떤 원하는 것을 공부하기 위해 필요한 것들을 공부하는 것 추천

Today I Felt

부딪히며 배우기

오늘 마스터 클래스에서 임성빈 교수님께서 기초를 전부 공부하고 머신러닝을 공부하는 것보다 원하는 것을 공부하기 위해 필요한 것을 공부하는 자세를 추천하셨다. 이렇게 공부하면 목적이 있기 때문에 더 강한 의지로 공부할 수 있을 것 같아 더 와닿았다. 다른 말로는 부딪히면서 배우라는 말씀같다고 느꼈다. 부스트캠프를 하기 전에는 AI 공부에 대해 하고 싶었지만 선형대수도 모르고 영어도 부족하고 등등 다양한게 부족해서 공부할 수 없다는 핑계를 댔었다. 하지만 이제는 그냥 하고 싶으면 뛰어드는게 맞다는 생각이 든다.

Ustage Day 10

목차