Pandas(2)

Groupby

SQL groupby 명령어와 같음
split → apply → combine
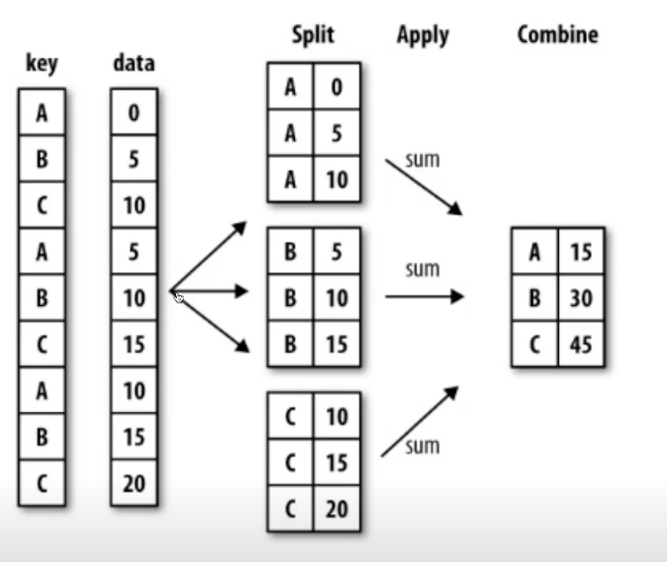
문법
- df.groupby(“Team”)[‘Point’].sum()
- df 데이터에서 팀별로 점수를 합산해서 구분해라.

import pandas as pd
ipl_data = {'Team': ['Riders', 'Riders', 'Devils', 'Devils', 'Kings',
         'kings', 'Kings', 'Kings', 'Riders', 'Royals', 'Royals', 'Riders'],
         'Rank': [1, 2, 2, 3, 3,4 ,1 ,1,2 , 4,1,2],
         'Year': [2014,2015,2014,2015,2014,2015,2016,2017,2016,2014,2015,2017],
         'Points':[876,789,863,673,741,812,756,788,694,701,804,690]}

df = pd.DataFrame(ipl_data)
df
'''
Team	Rank	Year	Points
0	Riders	1	2014	876
1	Riders	2	2015	789
2	Devils	2	2014	863
3	Devils	3	2015	673
4	Kings	3	2014	741
5	kings	4	2015	812
6	Kings	1	2016	756
7	Kings	1	2017	788
8	Riders	2	2016	694
9	Royals	4	2014	701
10	Royals	1	2015	804
11	Riders	2	2017	690
'''

df.groupby("Team")["Points"].sum()
'''
Team
Devils    1536
Kings     2285
Riders    3049
Royals    1505
kings      812
Name: Points, dtype: int64
'''

df = df.groupby(["Team", "Year"])["Points"].sum()
df
'''
Team    Year
Devils  2014    863
        2015    673
Kings   2014    741
        2016    756
        2017    788
Riders  2014    876
        2015    789
        2016    694
        2017    690
Royals  2014    701
        2015    804
kings   2015    812
Name: Points, dtype: int64
'''

엑셀의 피벗테이블로도 할 수 있음

Hierarchical index

여러 인덱스를 데이터프레임 조회에 넣어서 해당 인덱스들 기준으로 보는 방법
위 그룹바이 마지막 예시도 마찬가지
unstack() : 시리즈는 데이터프레임으로, 데이터프레임은 시리즈로 돌려줌
reset_index() : 다른 인덱스로 구성된 시리즈나 데이터프레임을 기본인덱스 데이터프레임으로 돌려줌

df2 = df.unstack()
df2

'''
Year	2014	2015	2016	2017
Team				
Devils	863.0	673.0	NaN	NaN
Kings	741.0	NaN	756.0	788.0
Riders	876.0	789.0	694.0	690.0
Royals	701.0	804.0	NaN	NaN
kings	NaN	812.0	NaN	NaN
'''

df3 = df.reset_index()
df3
'''
Team	Year	Points
0	Devils	2014	863
1	Devils	2015	673
2	Kings	2014	741
3	Kings	2016	756
4	Kings	2017	788
5	Riders	2014	876
6	Riders	2015	789
7	Riders	2016	694
8	Riders	2017	690
9	Royals	2014	701
10	Royals	2015	804
11	kings	2015	812
'''

swap_level() : 인덱스 순서(계층) 를 바꿔줌
sort_index() : 인덱스 기준 정렬
sort_values() : 값 기준 정렬

grouped

그룹바이에 의해 스플릿된 상태 추출
튜플로 키, 밸류가 엮여서 나옴
따로 함수는 아니고 groupby 로 나온 제너레이터 활용하는 방법임
타입은 pd.DataFrame.Groupby

grouped = df.groupby("Team")
for gr in grouped:
    print(gr)
'''
('Devils', Team    Year
Devils  2014    863
        2015    673
Name: Points, dtype: int64)
('Kings', Team   Year
Kings  2014    741
       2016    756
       2017    788
Name: Points, dtype: int64)
('Riders', Team    Year
Riders  2014    876
        2015    789
        2016    694
        2017    690
Name: Points, dtype: int64)
('Royals', Team    Year
Royals  2014    701
        2015    804
Name: Points, dtype: int64)
('kings', Team   Year
kings  2015    812
Name: Points, dtype: int64)
'''

for name, group in grouped:
    print(name)
    print(group)
'''
Devils
Team    Year
Devils  2014    863
        2015    673
Name: Points, dtype: int64
Kings
Team   Year
Kings  2014    741
       2016    756
       2017    788
Name: Points, dtype: int64
Riders
Team    Year
Riders  2014    876
        2015    789
        2016    694
        2017    690
Name: Points, dtype: int64
Royals
Team    Year
Royals  2014    701
        2015    804
Name: Points, dtype: int64
kings
Team   Year
kings  2015    812
Name: Points, dtype: int64
'''

grouped.get_group() : 특정 그룹 가져옴

grouped.get_group("Kings")
'''
Team   Year
Kings  2014    741
       2016    756
       2017    788
Name: Points, dtype: int64
'''

grouped 된 상태는 세 가지 유형의 apply 가능
- Aggregation : 요약된 통계정보 추출

grouped.agg(sum)
'''
Team
Devils    1536
Kings     2285
Riders    3049
Royals    1505
kings      812
Name: Points, dtype: int64
'''

# 여러 개도 가능
grouped.agg([sum, np.mean, max])
'''
sum	mean	max
Team			
Devils	1536	768.000000	863
Kings	2285	761.666667	788
Riders	3049	762.250000	876
Royals	1505	752.500000	804
kings	812	812.000000	812
'''

Transformation : group 된 데이터에서 해당 함수대로 모든 행에 적용, 그룹 별 연산에서 각각의 값에 영향 주고 싶을 때 사용

score = lambda x: (x - x.mean()) / x.std()
grouped.transform(score)
'''
Rank	Year	Points
-1.500000	-1.161895	1.284327
0.500000	-0.387298	0.302029
-0.707107	-0.707107	0.707107
0.707107	0.707107	-0.707107
1.154701	-1.091089	-0.860862
NaN	NaN	NaN
-0.577350	0.218218	-0.236043
-0.577350	0.872872	1.096905
0.500000	0.387298	-0.770596
0.707107	-0.707107	-0.707107
-0.707107	0.707107	0.707107
0.500000	1.161895	-0.815759
'''

Filteration : 특정 정보 제거해서 보여주는 필터기능

df.groupby('Team').filter(lambda x: x["Points"].max() > 800)
'''
Team	Rank	Year	Points
0	Riders	1	2014	876
1	Riders	2	2015	789
2	Devils	2	2014	863
3	Devils	3	2015	673
5	kings	4	2015	812
8	Riders	2	2016	694
9	Royals	4	2014	701
10	Royals	1	2015	804
11	Riders	2	2017	690
'''

컬럼의 데이터 타입 바꾸기

apply 사용

import dateutil

df_phone = pd.read_csv("./data/phone_data.csv")
df_phone.head()
'''
index	date	duration	item	month	network	network_type
0	0	15/10/14 06:58	34.429	data	2014-11	data	data
1	1	15/10/14 06:58	13.000	call	2014-11	Vodafone	mobile
2	2	15/10/14 14:46	23.000	call	2014-11	Meteor	mobile
3	3	15/10/14 14:48	4.000	call	2014-11	Tesco	mobile
4	4	15/10/14 17:27	4.000	call	2014-11	Tesco	mobile
'''

df_phone["date"] = df_phone["date"].apply(dateutil.parser.parse, dayfirst=True)
df_phone.dtypes
'''
index                    int64
date            datetime64[ns]
duration               float64
item                    object
month                   object
network                 object
network_type            object
dtype: object
'''

plot

matplotlib 설치
- !conda install - - y matplotlib
DF 나 시리즈 뒤에 .plot() 해주면 그림 나옴, 따로 임포트 안해도 됨

Pivot Table

엑셀의 기능과 같음
index 축은 groupby 와 동일
column 에 추가로 라벨링 값 추가하여 value 에 numeric 타입 값을 aggregation 하는 형태

df_phone.pivot_table(
    values=["duration"],
    index=[df_phone.month, df_phone.item],
    columns=df_phone.network,
    aggfunc="sum",
    fill_value=0,
)
'''
duration
network	Meteor	Tesco	Three	Vodafone	data	landline	special	voicemail	world
month	item									
2014-11	call	1521	4045	12458	4316	0.000	2906	0	301	0
data	0	0	0	0	998.441	0	0	0	0
sms	10	3	25	55	0.000	0	1	0	0
2014-12	call	2010	1819	6316	1302	0.000	1424	0	690	0
data	0	0	0	0	1032.870	0	0	0	0
sms	12	1	13	18	0.000	0	0	0	4
2015-01	call	2207	2904	6445	3626	0.000	1603	0	285	0
data	0	0	0	0	1067.299	0	0	0	0
sms	10	3	33	40	0.000	0	0	0	0
2015-02	call	1188	4087	6279	1864	0.000	730	0	268	0
data	0	0	0	0	1067.299	0	0	0	0
sms	1	2	11	23	0.000	0	2	0	0
2015-03	call	274	973	4966	3513	0.000	11770	0	231	0
data	0	0	0	0	998.441	0	0	0	0
sms	0	4	5	13	0.000	0	0	0	3
'''

# groupby 로 구현
df_phone.groupby(["month", "item", "network"])["duration"].sum().unstack()
'''
network	Meteor	Tesco	Three	Vodafone	data	landline	special	voicemail	world
month	item									
2014-11	call	1521.0	4045.0	12458.0	4316.0	NaN	2906.0	NaN	301.0	NaN
data	NaN	NaN	NaN	NaN	998.441	NaN	NaN	NaN	NaN
sms	10.0	3.0	25.0	55.0	NaN	NaN	1.0	NaN	NaN
2014-12	call	2010.0	1819.0	6316.0	1302.0	NaN	1424.0	NaN	690.0	NaN
data	NaN	NaN	NaN	NaN	1032.870	NaN	NaN	NaN	NaN
sms	12.0	1.0	13.0	18.0	NaN	NaN	NaN	NaN	4.0
2015-01	call	2207.0	2904.0	6445.0	3626.0	NaN	1603.0	NaN	285.0	NaN
data	NaN	NaN	NaN	NaN	1067.299	NaN	NaN	NaN	NaN
sms	10.0	3.0	33.0	40.0	NaN	NaN	NaN	NaN	NaN
2015-02	call	1188.0	4087.0	6279.0	1864.0	NaN	730.0	NaN	268.0	NaN
data	NaN	NaN	NaN	NaN	1067.299	NaN	NaN	NaN	NaN
sms	1.0	2.0	11.0	23.0	NaN	NaN	2.0	NaN	NaN
2015-03	call	274.0	973.0	4966.0	3513.0	NaN	11770.0	NaN	231.0	NaN
data	NaN	NaN	NaN	NaN	998.441	NaN	NaN	NaN	NaN
sms	NaN	4.0	5.0	13.0	NaN	NaN	NaN	NaN	3.0
'''

Crosstab

피벗테이블과 거의 동일
네트워크 데이터 (a 와 b 가 상관 있음) 에 사용하면 편함
인덱스, 컬럼, 벨류, 어그리게이션 세팅 하면됨

→ groupby, pivot_table, crosstab 다 가능

merge & concat

merge (join 과 같음)

sql 에서 많이 사용하는 merge 와 같은 기능
두 개의 테이블을 하나로 합침
기준이 있어야함
pd.merge(df_a, df_b, on=’subject_id’) # 두 테이블을 subject_id 를 기준으로 합침
두 테이블에서 컬럼명이 다를 때는 left_on 과 right_on 따로 적어주면 됨
join method
- inner join : 겹치는 내용만 보여줌
- full join : 모든 내용 다 합쳐서 보여줌
- left join : 왼쪽 모든 내용 + 오른쪽 겹치는 내용 보여줌
- right join : left join 반대
- 없는 값은 NaN 으로 채워짐
- merge(~~, how=”inner”) 로 적어주면 됨, 기본은 inner

concat

컬럼을 더 넓히는게 아니라 데이터 양을 더 넓힘 (세로로) → 같은 컬럼을 갖고 있어야함
axis=1 하면 옆으로 붙음
pd.concat([df_a, df_b])

=> 여러 엑셀 파일들 합치고 필요한 정보 뽑을 때 groupby merge concat 등등 쓰면 유용

Persistance

DB 연결

sqlite3

로컬 디비
import sqlite3 해서 써도 됨
원격 되는 mysql 등 써도 됨

엑셀 작성기

!conda install —y XlsxWriter
- df_routes 사용가능
writer = pd.ExcelWriter(…) 쓰고 df_routes.to_excel(writer, sheet_name=”my_data”) 하면 작성가능
df_routes.to_pickle 가능

확률론 맛보기

딥러닝에서 확률론이 필요한 이유

딥러닝은 확률론 기반의 기계학습 이론에 기반함
손실함수 (loss function) 들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도함
- 예측이 틀릴 위험 (risk) 를 최소화하도록 데이터를 학습 → SGD
회귀 분석에서 손실함수로 사용되는 L2-norm 은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도
분류 문제에서 사용되는 교차엔트로피 (cross-entropy) 는 모델 예측의 불확실성을 최소화하는 방향으로 학습
분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 알아야 함
- 두 대상을 측정하는 방법은 통계학 기반이므로 확률론을 알아야 함

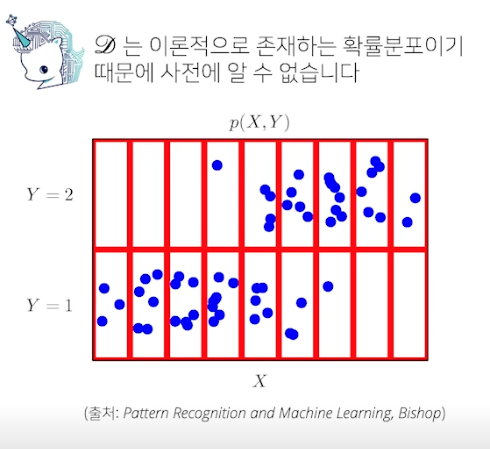
확률분포는 데이터의 초상화

테이터 공간을 $x$ x $y$ 라 표기하고 𝔇 는 데이터공간에서 데이터를 추출하는 분포
데이터는 확률변수로 ($x$, $y$) ~ 𝔇 라 표기
- 확률변수는 함수로 표시, 임의로 데이터 공간에서 관측된 데이터를 확률변수로 데이터 추출
- 추출한 데이터의 분포 → 𝔇
결합분포 P(x, y) 는 𝔇 를 모델링
- 결합분포는 원래 확률분포 타입에 상관없이 이산형이나 연속형 가능
- 결합분포는 아규먼트로 쓰인 확률변수들을 같이 고려한다는 뜻
P(x) 는 입력 x 에 대한 주변확률분포로 y 에 대한 정보를 주지 않음
- 주변확률분포 P(x) 는 결합분포 P(x, y) 를 y 에 대해 더하거나 적분해서 유도
조건부확률분포 P(x | y) 는 데이터 공간에서 입력 x 와 출력 y 사이의 관계를 모델링
- P(X | Y = 1) : Y 가 1 일 때 X 의 확률분포
- 원딜님 설명 : 전체 공간 S 대신 Y 공간에서 X 의 확률분포
- 결합분포말고 조건부확률분포를 쓰면 데이터 각각에 대해 더 명확하게 알아낼 수 있음
확률분포는 데이터를 해석하는데 도움을 줌 (초상화)

이산확률변수 vs 연속확률변수

확률변수는 확률분포 𝔇 에 따라 이산형 (discrete) 과 연속형 (continuous) 확률변수로 구분
- 데이터 공간 $x$ x $y$ 로 구분하는게 아니라 확률분포의 종류에 따라 구분!
이산형확률변수
- 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링함
- P(X = x) 는 확률변수가 x 값을 가질 확률
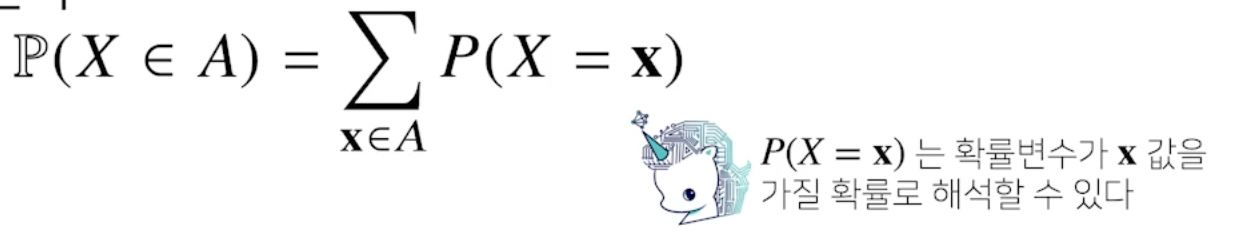
연속형확률변수
- 데이터 공간에 정의된 확률변수의 밀도 (density) 위에서의 적분을 통해 모델링
- P(x) : 밀도함수, 누적확률분포, 데이터 공간에 정의된 확률보다는 밀도 (적분 필요)
  - 밀도는 누적확률분포의 변화율을 모델링, 확률로 해석 x
- 보통 컴퓨터에 쓰는 데이터는 이산형이지만 기계학습에는 정규분포, 감마분포 등 연속형확률변수 씀
이산형과 연속형으로 모든 확률분포 표현되는건 아님, 더 있음

조건부확률과 기계학습

조건부확률 P(y | x) 는 입력변수 x 에 대해 정답이 y 일 확률
- 연속확률분포면 확률 대신 밀도로 해석
저번 시간에 사용한 로지스틱 회귀의 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률 해석
- 선형함수가 비선형함수를 거치면 확률이 됨
분류 문제에서 softmax($W\phi + b)$ 는 데이터 x 로부터 추출된 특징패턴 $\phi(x)$ 과 가중치행렬 W 을 통해 조건부 확률 P(y | x) (= P(y | $\phi(x)$) 를 계산
회귀 문제의 경우 조건부기대값 E[y | x] 를 추정
- 조건부 확률 대신 조건부기대값을 구해야(추정)한다는 말
- 보통 회귀 문제는 연속확률분포를 다루므로 적분 사용
- 왜 조건부기대값을 구하나?
  - 목적식 L2-norm 을 최소화하는 함수 = 조건부기대값 이기 때문
- robust (강건) 하게 예측할 때는 조건부기대값 대신 median (중간값) 사용
- 통계적 모형에서 원하는 목적에 따라 추정량이 달라질 수 있다!
딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴 $\phi$ 를 추출
- 특징패턴을 학습하기 위해 어떤 손실함수를 사용할지는 기계학습 문제와 모델에 의해 결정됨

기대값

확률분포가 주어지면 데이터를 분석하는데 사용 가능한 여러 종류의 통계적 범함수 (statistical function) 계산 가능
기대값 (expectation) 은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는데 사용

기대값을 이용해 분산, 첨도(첨도말고 왜도인듯 = 비대칭도), 공분산 등 여러 통계량 계산 가능

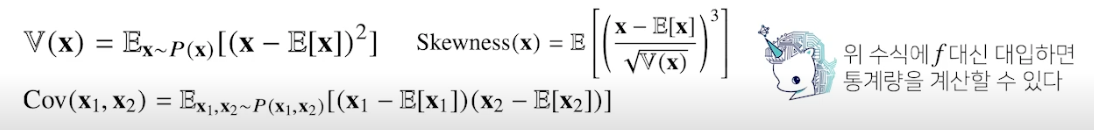
기억해야할 것 : 이산이면 급수(질량함수), 연속이면 적분 사용

몬테카를로 샘플링

기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분 → 몬테카를로 샘플링은 기계학습에서 매우 다양하게 응용
확률분포를 모르기에 데이터를 이용해 기대값을 계산하기 위해 몬테카를로 샘플링을 사용
이산형 연속형 상관없이 성립
독립추출 (분포에서 독립적으로 추출 = 샘플링) 이 보장된다면 대수의 법칙 (law of large number) 에 의해 수렴성을 보장
(Q. 대수의 법칙이 뭐지 -> 전체 모집단에서 랜덤한 표본의 평균은 전체의 평균과 가까울 가능성이 높다는 법칙)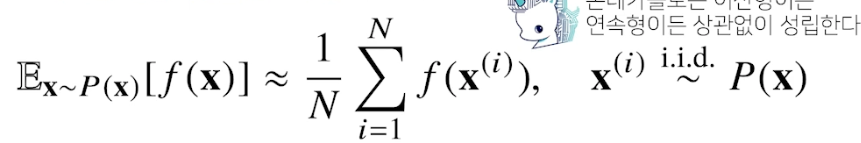
예제 : 적분 계산하기
- 확률분포가 아닌 공간에서 적분은 불가능 → 몬테카를로
- 예제의 f(x) 는 우리가 아는 적분식으로 적분 구하기 힘듦
- f(x) 의 적분의 길이가 2 이므로 반으로 나누면 기대값. 기대값은 몬테카를로 방법 가능.
- 다 구하고 다시 2 곱하면 됨.
- uniform (균등) 분포에서 샘플링해주면 오차 범위 안에 들어옴.
  - 샘플 사이즈가 적으면 오차범위 커짐 → 참값에 멀어짐, 적절히 조절해야 함

피어 세션

피어 세션이 피어씁니다

각오 : 우리 나이에 늦은건 키즈 모델뿐! 초심과 맥심을 잃지 말자^^

수업 질문

iid = 서로 독립이고 동일한 분포를 따른다. ~ 물결 표시로 표현. 이게 돼야 몬테카를로 샘플링 가능 (전제조건임)
확률 배우고 이런거 실제로 많이 쓰일까?
→ 논문 볼 때 수식 엄청 나와서 모르면 이해가 안됨
펭귄님 블로깅 팁 : 아웃라인 먼저 막 적어놓고 정리를 해나감
서폿님 : 수식을 인식해서 라텍스 문법으로 바꿔주는 프로젝트 해보고 싶다 (OCR)
→ 엠제이님 : mask RCNN 논문 읽어보는거 추천

Today I Felt

조화

2 주차는 머신러닝에 필요한 수학에 대해 공부하고 있다. 수학에 관련되다보니 요즘 피어세션에서 가장 두드러지는 사람은 원딜님이다 (통계갓,,) . 통계에 대한 기본 지식도 정리해서 올려주고 피어 세션에 나오는 질문도 잘 알려주고 계신데, 우리 조에 컴공만이 아니라 통계학과 수학과 등 여러 환경의 사람들이 모였기 때문에 더 도움 받기 좋음을 느꼈다. 왜 요즘 회사들도 비전공자 출신을 뽑는지 알 것 같았다. 기본 실력만 있다면 다채로움이 만들어내는 조화가 더 좋기 때문이 아닐까?

Ustage Day 9

목차