목차
경사하강법(순한맛)
미분
- 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 가장 많이 사용
- 변화율의 극한
- $f^{`}(x) = \lim_\mathit{h\rightarrow0}(f(x+h)-f(x))/h$
- 파이썬에서
sympy모듈의sympy.diff를 사용해 미분 계산 가능
import sympy as sym
from sympy.abc import x # 라틴-그리스 문자 중 x 사용
sym.diff(sym.poly(x**2 + 2*x + 3), x) # 첫 인자 : 수식, 두번째 인자 : 미분 대상
# Poly(2𝑥+2,𝑥,𝑑𝑜𝑚𝑎𝑖𝑛=ℤ)
sympy는 파이썬에서 제공하는 기호 처리 모듈이다.LaTeX수식을 지원하기 때문에 여러 수식이나 문자에 대해 처리해준다. 또한sympy로 함수를 얻고numpy로 처리하는 식으로 함께 사용한다.- 미분을 그림으로 보자면, f 함수의 그래프의 어떤 점 (벡터) 에서 접선의 기울기이다.
- 미분을 어디에 쓸까?
- 함수에 주어진 점 (x, f(x)) 에서 접선의 기울기를 구함
- 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가하는지 or 감소하는지 알 수 있다. (차원이 많을 때 특히 유용)
- 함수값을 증가시키고 싶으면, 기존 함수값에 미분값을 더한다. (Gradient-ascent, 경사상승법, 극대값의 위치를 구할 때 사용)
- 함수값을 감소시키고 싶으면, 기존 함수값에 미분값을 뺀다. (Gradient-descent, 경사하강법, 극소값의 위치를 구할 때 사용)
- 극 값에 도달하면 움직임을 멈춤 (최적화 완료)
경사하강법
- 변수 1 개일 때
# gradient : 미분 계산 함수
# init : 시작점, lr : 학습률, eps : 알고리즘 종료조건
var = init
grad = gradient(var)
while (abs(grad) > eps):
var = var - (lr * grad)
grad = gradient(var)
- 변수가 벡터라면? (변수가 여러개)
- 벡터가 입력인 다변수 함수의 경우 편미분 사용
- 편미분
- 단위 벡터를 이용해서 특정 벡터 원소만 변화율을 구함
- 특정 변수만 변수 취급하고 나머지는 상수 취급하여 미분
import sympy as sym from sympy.abc import x, y sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2*y), x) # 2𝑥+2𝑦−sin(𝑥+2𝑦) - 각 변수별로 편미분을 계산한 그레디언트 (gradient) 벡터를 이용하여 경사하강/상승법에 사용할 수 있음
- 그레디언트 벡터 (역삼각형 기호 : nabla, 편미분 기호 : round d)
- $\nabla f = (\partial_\mathit{x1}f, \partial_\mathit{x2}f, …, \partial_\mathit{xd}f)$
- 그레디언트 벡터에 마이너스를 붙인 그래프를 보면 밑으로 움푹패인 모양이 나옴 → 임의의 점에서 극소점으로 향하는 방향을 알 수 있게됨
- 그레디언트 벡터 (역삼각형 기호 : nabla, 편미분 기호 : round d)
- 그레디언트 벡터를 사용한 경사하강법 알고리즘
# 위에 있는 변수 하나에 대한 경사하강법과 거의 같음, 그레디언트 벡터는 절대값을 씌울 수 없기 때문에 norm (크기) 를 구함
# gradient : 그레디언트 벡터를 계산하는 함수
# init : 시작점, lr : 학습률, eps : 알고리즘 종료조건
var = init
grad = gradient(var)
while (norm(grad) > eps):
var = var - (lr * grad)
grad = gradient(var)
경사하강법(매운맛)
선형회귀분석 복습
- n 개의 변수 데이터에 대해 이를 가장 잘 표현하는 선을 찾는 방법
- 데이터가 차원보다 많기 때문에 무어-펜로즈 역행렬을 이용해야함
- y_hat (주어진 y 와 가장 비슷한 선형)
- 이번 시간에는 무어-펜로즈 역행렬 이용하지 않고 경사하강법을 이용해서 적절한 선형모델을 찾을 것! (이 방법이 기계학습에서 더 일반적)
경사하강법으로 선형회귀 계수 구하기
- 선형회귀 목적식 : $|y - X\beta |_2$ ($|$ : 벡터의 크기 (노름), 옆에 밑숫자 : L-1or2 노름)
- 목적식에 대한 그레디언트 벡터를 구해야함, 목적식을 최소화하는 $\beta$ 를 찾기 위해
-
기존 L2 노름과 다른 점은 n 개의 데이터로 계산하기 때문에 평균값을 구해주기 위해 제곱 시그마에 n 을 나눔

- t+1 번째 $\beta$ 는 t 번째 $\beta$ - lr * t 번째 그레디언트 벡터 이다.
-
그레디언트 벡터 구할 때, 제곱을 이용하면 더 편리함

- 경사하강법 기반 선형회귀 알고리즘
# norm : L2-노름을 계산하는 함수
# lr : 학습률, T : 학습횟수, beta : 예측값
for t in range(T):
error = y - X @ beta
grad = - transpose(X) @ error
beta = beta - lr * grad
- 예시
import numpy as np
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3
lr = 0.01
beta_gd = [10.1, 15.1, -5] # [1, 2, 3] 이 정답
X_ = np.array([np.append(x, [1]) for x in X]) # intercept 항 추가
for t in range(5000):
error = y - X_ @ beta_gd
# error = error / np.linalg.norm(error)
grad = - np.transpose(X_) @ error
beta_gd = beta_gd - lr * grad
print(beta_gd)
- lr 을 잘 맞춰줘야 함, 너무 작으면 수렴 못하고, 너무 크면 부호가 바껴버림
경사하강법은 만능일까?
- 이론적으로 미분가능한 볼록 (convex) 함수에 대해서는 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장됨
- 특히 선형회귀의 경우 목적식이 회귀계수 $\beta$ 에 대해 볼록함수 이기 때문에 수렴 보장
- 하지만 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 (non-convex ) 수렴이 항상 보장되지 않음
확률적 경사하강법
- SGD (Stochastic Gradient Descent) 는 모든 데이터를 사용해서 업데이트 하는게 아니라 데이터를 한 개 또는 일부만 활용하여 경사하강법 써서 업데이트
- non-convex 목적식은 SGD 를 통해 최적화할 수 있음
-
미니 배치 방식으로 사용

-
데이터를 전체가 아닌 일부로 파라미터를 업데이트하기 때문에 연산자원을 좀 더 효율적으로 활용하는데 도움이 됨

- 원리 : 미니배치 연산
- 미니배치로 그레디언트 벡터를 계산, 미니배치는 확률적으로 선택하므로 목적식 모양이 바뀜
- 넌컨벡스 함수에서 전체 데이터를 사용하는 경사하강법을 사용했을 때 극소점을 발견못하고 갇혀버리는 반면, 미니배치를 사용하면 여러개의 저점을 찾아내기 때문에 극소점을 발견할 수 있음
-
경사하강법은 직선처럼 내려가지만, SGD 는 지그재그하면서 찾아다님
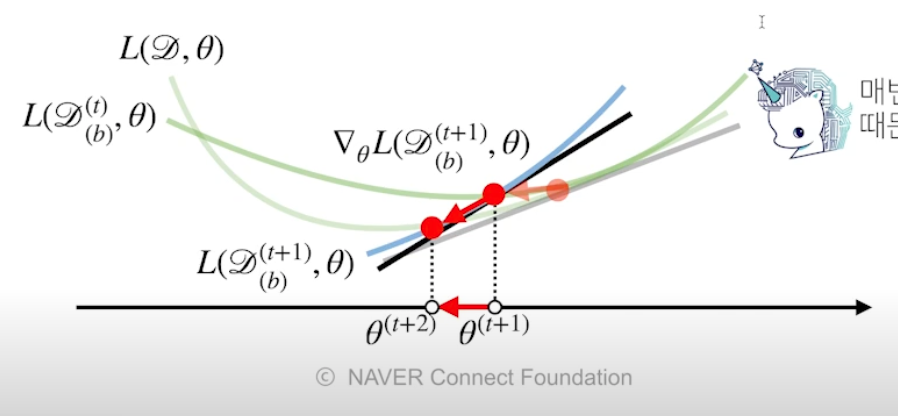
- 경사하강법보다 SGD 가 더 머신러닝에 적합함
- 미니배치 사이즈도 잘 맞춰야함, 너무 느려질 수 있기 때문
- 하드웨어적으로도 SGD 를 써야함, 이미지 데이터 2^37 짜리를 한 번에 돌리는건 메모리가 감당 못하기 때문에 미니배치로 쪼개서 해야함 ⇒ 빠르면서 하드웨어 한계 극복(병렬 연산) 가능
교수님 말씀
- 경사하강법 알고리즘 수식 정확히 이해하기
- 확률적 경사하강법 충분히 이해하기
피어 세션
수업 관련 질문
- 경사하강법 선형회귀를 코드로 구현할 때 X 행렬에 인터셉트행으로 왜 1 을 추가할까요?
- SGD 에서 1 에포크는 전체 데이터중 일부를 추출하여 돌리는 것일까요? 아니면 전체 데이터를 랜덤하게 나눠서 다 돌리는걸까요?
Today I Felt
모르면 처음부터
어제 배운 선형대수의 벡터, 행렬의 내적과 역행렬을 제대로 이해하지 못해 오늘 수업의 개념까지 꼬여버렸다. 멘붕이지만 다시 어제 내용을 처음부터 이해하면서 개념을 익혀야겠다. 포기하지 말자.